| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 18) | Question 1 to 21 (Multiple Choice Questions) | Question 22 to 41 (Fill in the Blanks) |
| Question 42 to 61 (True or False) | Question 62 to 102 | |
Chapter 6 Visualising The Solid Shapes
Welcome to this dedicated resource offering comprehensive, step-by-step solutions for the NCERT Exemplar problems tailored for Class 8 Mathematics, focusing on the intriguing chapter: Visualising Solid Shapes (Chapter 10). These Exemplar questions are intentionally designed to move beyond simple identification of three-dimensional objects, pushing students to significantly strengthen their spatial reasoning abilities. This is achieved by presenting more complex 3D objects, exploring various methods of 2D representation, analyzing intricate nets, and applying fundamental topological properties like Euler's formula in diverse and challenging contexts.
The solutions provided meticulously cover the essential skills needed to understand and interpret the world of three dimensions. This includes:
- Identifying common 3D shapes such as cubes, cuboids, cylinders, cones, spheres, pyramids (like square pyramids or triangular pyramids), and prisms (like triangular prisms or pentagonal prisms).
- Understanding and correctly identifying the core components of these shapes: the flat surfaces known as faces (F), the line segments where faces meet called edges (E), and the points where edges meet known as vertices (V).
- Interpreting and drawing nets for various solids. A net is a 2D pattern that can be folded along its edges to form a 3D shape. Exemplar problems often challenge students not just to draw nets, but also to critically analyze given flat patterns and determine if they can actually be folded to create a specific closed solid without overlaps.
A crucial aspect of visualizing solid shapes is understanding how they can be represented on a two-dimensional plane. The solutions thoroughly address:
- Interpreting and drawing different 2D views of 3D objects. This primarily involves understanding and sketching the Top View, Front View, and Side View of solids, including combinations of basic shapes (like stacked cubes or a cone placed on a cylinder). Accurately visualizing the hidden parts and representing them correctly is a key skill tested.
- Understanding, if not always drawing complex versions of, other 2D representations like oblique sketches (which show depth but can distort angles) and isometric sketches (drawn on isometric dot paper, providing a more proportional pseudo-3D view). Interpretation of these sketches, especially for composite solids, is often a focus.
A cornerstone concept for polyhedrons (solids with flat faces, straight edges, and sharp vertices) explored in depth is Euler's Formula. This remarkable formula establishes a fundamental relationship between the number of faces, vertices, and edges of any simple, convex polyhedron. The solutions provide extensive guidance on applying this formula:
- The formula itself is $F + V - E = 2$.
- Verifying Euler's formula for various given polyhedra, including more complex ones, by carefully counting their faces, vertices, and edges.
- Using the formula algebraically to find the number of faces, vertices, or edges when the other two quantities are known (e.g., if $F=5$ and $V=6$, find $E$ using $5+6-E=2$).
- Determining if a given combination of F, V, and E values can actually correspond to a real polyhedron by checking if they satisfy Euler's formula $F+V-E=2$.
Catering to diverse question formats (MCQs, Fill-in-the-Blanks, True/False, Short/Long Answer), these solutions provide clear diagrams illustrating nets, views, and solids, demonstrate systematic methods for counting F, V, and E, and showcase the logical application of Euler's formula. Engaging with this resource will significantly improve students' ability to visualize 3D objects from 2D representations, understand the structure of solids, and appreciate the fundamental topological invariant captured by Euler's formula.
Solved Examples (Examples 1 to 18)
In examples 1 and 2, write the correct answer from the given four options.
Example 1: A prism is a polyhedron whose lateral faces are
(a) Circles
(b) Triangles
(c) Parallelograms
(d) Rhombuses or Rhombi
Answer:
A prism is a polyhedron characterised by two parallel and congruent polygonal bases.
The faces connecting the corresponding sides of the two bases are the lateral faces.
These lateral faces are always parallelograms.
In a right prism, the lateral faces are rectangles, which are a special type of parallelogram.
Therefore, the lateral faces of a prism are parallelograms.
The correct option is (c) Parallelograms.
Example 2: A pyramid is a polyhedron whose lateral faces are
(a) Rectangles
(b) Triangles
(c) Parallelograms
(d) Rhombuses or Rhombi
Answer:
A pyramid is a polyhedron formed by connecting a polygonal base to a common point, called the apex.
The faces formed by connecting the sides of the base to the apex are the lateral faces.
Each side of the polygonal base serves as the base of a triangle, and the apex is the common vertex for all these triangles.
Therefore, the lateral faces of a pyramid are always triangles.
The correct option is (b) Triangles.
In examples 3 and 4, fill in the blanks to make the statements true
Example 3: In a regular polyhedron ______ number of faces meet at each vertex.
Answer:
A polyhedron is considered regular if its faces are all congruent regular polygons and the same number of faces meet at each vertex.
This property, where the same number of faces meet at each vertex, is a defining characteristic of regular polyhedra (along with congruent regular faces).
Therefore, the blank should be filled with the phrase describing this property.
In a regular polyhedron the same number of faces meet at each vertex.
Example 4: A pentagonal prism has ______ edges.

Answer:
A pentagonal prism has a pentagon as its base. A pentagon has 5 vertices and 5 edges.
A prism has two identical bases and lateral faces connecting corresponding sides.
Number of vertices in a pentagonal prism = Number of vertices in base $\times$ 2 = $5 \times 2 = 10$.
Number of faces in a pentagonal prism = Number of base faces + Number of lateral faces = $2 + 5 = 7$. (2 pentagonal bases and 5 parallelogram lateral faces).
To find the number of edges, we can count the edges on the bases and the lateral edges.
Edges on the two bases = Edges per base $\times$ 2 = $5 \times 2 = 10$.
Lateral edges (connecting the vertices of the two bases) = Number of vertices per base = $5$.
Total number of edges = Edges on bases + Lateral edges = $10 + 5 = 15$.
Alternatively, using Euler's formula for polyhedra: $V - E + F = 2$, where $V$ is vertices, $E$ is edges, and $F$ is faces.
We have $V=10$ and $F=7$.
Substituting these values: $10 - E + 7 = 2$
$17 - E = 2$
$E = 17 - 2 = 15$.
A pentagonal prism has 15 edges.
In examples 5 and 6, state whether the statements are true or false.
Example 5: A sphere is a polyhedron.
Answer:
A polyhedron is a three-dimensional solid object whose surface is made up of a finite number of polygonal faces.
Key characteristics of a polyhedron include having flat faces, straight edges, and vertices (corners).
A sphere is a perfectly round geometrical object in three-dimensional space.
The surface of a sphere is curved; it does not have any flat faces, straight edges, or vertices.
Since a sphere lacks the fundamental defining characteristics of a polyhedron (flat faces, straight edges, vertices), it is not a polyhedron.
The statement "A sphere is a polyhedron" is False.
Example 6: In a prism the lateral faces need not be congruent
Answer:
A prism is a polyhedron with two identical and parallel polygonal bases and lateral faces that are parallelograms.
The lateral faces connect corresponding sides of the two bases.
If the base polygon is irregular (i.e., its sides are not all equal in length), then the corresponding sides in the two bases will also have different lengths.
The lateral faces are parallelograms whose width is the length of the corresponding side of the base and whose height is the perpendicular distance between the bases (for a right prism) or the length of the lateral edge (for an oblique prism).
If the base has sides of different lengths, the lateral faces will be parallelograms with different base lengths, and thus they will not be congruent.
For example, a right prism with a rectangular base that is not a square will have two pairs of congruent rectangular lateral faces, but the two pairs will not be congruent to each other if the rectangle's length and width are different.
Therefore, it is true that the lateral faces of a prism need not be congruent.
The statement "In a prism the lateral faces need not be congruent" is True.
Example 7: Draw the top, front and side views of the given solid.
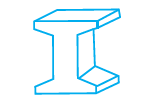
Answer:
The top, front, and side views of the given solid represent how the solid appears when viewed directly from above, from the front, and from one of the sides, respectively.
Front View:
Looking at the solid from the front, we observe a stepped structure. This view will show three rectangular areas stacked vertically, with each upper rectangle set back or forward relative to the one below it, creating a staircase profile.
Top View:
Looking down at the solid from above, we see the extent of the solid on the horizontal plane. This view will show the rectangular base and the outlines of the upper layers. It will appear as a set of concentric or aligned rectangles, showing the decreasing area covered at each successive level.
Side View:
Looking at the solid from the side (assuming the side perpendicular to the front view), we will see the overall rectangular outline of the solid from that perspective. The edges formed by the steps on the front view will appear as vertical lines within this rectangle in the side view, dividing it into vertical sections corresponding to the different depths of the steps.
Example 8: Use isometric dot paper to sketch a rectangular prism with length 4 units, height 2 units and width 3 units.
Answer:
Isometric dot paper provides a grid of dots arranged in equilateral triangles, which helps in drawing 3D objects in isometric projection. To sketch a rectangular prism, we need to represent its length, width, and height along the three isometric axes.
Follow these steps:
1. Choose a starting dot on the isometric paper. This will represent one vertex of the rectangular prism (e.g., a corner of the base).
2. From this starting dot, draw a line segment of length 4 units along one of the isometric grid directions (e.g., following the dots diagonally upwards and to the right). This represents the length of the prism.
3. From the same starting dot, draw a line segment of width 3 units along another isometric grid direction (e.g., following the dots diagonally upwards and to the left). This represents the width of the prism.
4. From the end point of the 4-unit line, draw a line segment of 3 units parallel to the width line drawn in step 3. From the end point of the 3-unit line, draw a line segment of 4 units parallel to the length line drawn in step 2. These two lines should meet, completing the base parallelogram of the prism.
5. From each of the four vertices of the base parallelogram, draw a vertical line segment upwards, each of height 2 units (following the vertical grid lines). This represents the height of the prism.
6. Connect the top end points of these vertical line segments. The resulting figure at the top will be a parallelogram congruent to the base parallelogram. The edges connecting the top vertices should be parallel to the corresponding base edges.
7. For clarity, you can draw the visible edges with solid lines and the hidden edges (usually the three edges on the back side) with dashed lines.
The resulting sketch on the isometric dot paper will be an isometric view of the rectangular prism with the specified dimensions.
Example 9: Identify the shape whose net is given below.

Answer:
The given figure is a net, which is a 2D pattern that can be folded to form a 3D object.
Let's examine the components of the net.
The net consists of six congruent square faces arranged in a specific pattern.
When this net is folded along the edges, the squares will form the faces of a three-dimensional shape.
A polyhedron with six congruent square faces is known as a cube.
The shape whose net is given is a cube.
Example 10: The solid given below is a rectangular prism or cuboid. Make all the diagonals of this shape.

Answer:
A rectangular prism, or cuboid, is a polyhedron with 6 rectangular faces, 12 edges, and 8 vertices.
Diagonals in a cuboid are line segments connecting two vertices that are not on the same face.
There are two types of diagonals in a cuboid: face diagonals and space diagonals.
Face Diagonals:
These are the diagonals drawn on each of the rectangular faces. Each rectangular face has two diagonals.
A cuboid has 6 faces.
Number of face diagonals = Number of faces $\times$ Diagonals per face
Number of face diagonals = $6 \times 2 = 12$.
On the given figure, these would be lines like AC, BD (on the bottom face), EG, FH (on the top face), AB', DC' (on one side face), AD', BC' (on another side face), AE, BF (on the front face), CG, DH (on the back face), where B', C', D' represent the vertices on the back or side not labelled in the diagram, or using the likely vertex labels A, B, C, D for the base and E, F, G, H for the top (with E above A, F above B, etc.), the face diagonals are AC, BD, EG, FH, AF, BE, CG, DH, AH, DE, BG, CF.
Space Diagonals:
These are the diagonals that pass through the interior of the cuboid, connecting opposite vertices.
There are 4 space diagonals in a cuboid.
These connect vertex pairs (A, G), (B, H), (C, E), (D, F) based on the standard labeling where A,B,C,D form the base and E,F,G,H form the top corresponding to A,B,C,D respectively.
On the given figure (assuming A, B, C, D are bottom vertices and E, F, G, H are top vertices, e.g., A is bottom left front, B is bottom right front, D is bottom left back, C is bottom right back, and E, F, H, G are top corresponding vertices), the space diagonals are AG, BH, CE, DF.
Total Diagonals:
Total number of diagonals = Number of face diagonals + Number of space diagonals
Total number of diagonals = $12 + 4 = 16$.
To make (draw) all the diagonals on the shape, one would draw these 16 line segments connecting the appropriate pairs of vertices.
Example 11: Count the number of cubes in the given shapes.

Answer:
To count the number of cubes in the given shapes, we can examine the structures layer by layer from the base or count the cubes in each visible column.
Shape 1 (Left Structure):
Let's count layer by layer from the bottom.
The bottom layer appears to be a complete $3 \times 3$ square arrangement.
Number of cubes in Layer 1 = $3 \times 3 = 9$.
The second layer sits on top of the central $2 \times 2$ section of the first layer.
Number of cubes in Layer 2 = $2 \times 2 = 4$.
The third layer sits on top of the central $1 \times 1$ section of the second layer.
Number of cubes in Layer 3 = $1 \times 1 = 1$.
Total number of cubes in Shape 1 = Sum of cubes in all layers = $9 + 4 + 1 = 14$.
Shape 2 (Right Structure):
Let's count the height of the stacks in each position of the $2 \times 2$ base.
From the viewing angle, we can see four vertical stacks (columns).
The front-left stack has a height of 3 cubes.
The front-right stack has a height of 3 cubes.
The back-left stack has a height of 3 cubes.
The back-right stack has a height of 1 cube.
Total number of cubes in Shape 2 = Sum of cubes in all stacks = $3 + 3 + 3 + 1 = 10$.
Number of cubes in Shape 1 is 14.
Number of cubes in Shape 2 is 10.
Example 12: Name the following polyhedrons and verify the Euler’s formula for each of them.

Answer:
We need to identify each polyhedron and then count its vertices ($V$), edges ($E$), and faces ($F$) to verify Euler's formula $V - E + F = 2$.
Polyhedron (i):
This polyhedron has a triangular base and three triangular lateral faces that meet at a single apex.
This shape is a triangular pyramid (also known as a tetrahedron).
Let's count the vertices, edges, and faces:
Vertices ($V$): There are 3 vertices on the base and 1 apex vertex. So, $V = 3 + 1 = 4$.
Edges ($E$): There are 3 edges on the base and 3 lateral edges connecting the base vertices to the apex. So, $E = 3 + 3 = 6$.
Faces ($F$): There is 1 triangular base face and 3 triangular lateral faces. So, $F = 1 + 3 = 4$.
Now, let's verify Euler's formula $V - E + F = 2$:
$V - E + F = 4 - 6 + 4 = 8 - 6 = 2$.
Since $V - E + F = 2$, Euler's formula is verified for the triangular pyramid.
Polyhedron (ii):
This polyhedron has two identical rectangular bases that are parallel and congruent. The lateral faces are parallelograms (or rectangles in this case, appearing as a right prism).
This shape is a rectangular prism (also known as a cuboid).
Let's count the vertices, edges, and faces:
Vertices ($V$): There are 4 vertices on the bottom base and 4 corresponding vertices on the top base. So, $V = 4 + 4 = 8$.
Edges ($E$): There are 4 edges on the bottom base, 4 edges on the top base, and 4 vertical lateral edges connecting the bases. So, $E = 4 + 4 + 4 = 12$.
Faces ($F$): There are 2 rectangular base faces (bottom and top) and 4 rectangular lateral faces. So, $F = 2 + 4 = 6$.
Now, let's verify Euler's formula $V - E + F = 2$:
$V - E + F = 8 - 12 + 6 = 14 - 12 = 2$.
Since $V - E + F = 2$, Euler's formula is verified for the rectangular prism.
Example 13: A polyhedron has 7 faces and 10 vertices. How many edges does the polyhedron have?
Answer:
We are given the number of faces ($F$) and the number of vertices ($V$) of a polyhedron, and we need to find the number of edges ($E$).
We can use Euler's formula for polyhedra, which relates the number of vertices, edges, and faces:
$\qquad V - E + F = 2$
Given:
Number of faces, $F = 7$
Number of vertices, $V = 10$
We need to find $E$.
Substitute the given values into Euler's formula:
$10 - E + 7 = 2$
... (i)
Combine the constant terms on the left side:
$17 - E = 2$
To find $E$, rearrange the equation:
$E = 17 - 2$
Calculate the value of $E$:
$E = 15$
The polyhedron has 15 edges.
Example 14: Find the number of vertices in a polyhedron which has 30 edges and 12 faces.
Answer:
We are given the number of edges ($E$) and the number of faces ($F$) of a polyhedron, and we need to find the number of vertices ($V$).
We can use Euler's formula for polyhedra, which relates the number of vertices, edges, and faces:
$\qquad V - E + F = 2$
Given:
Number of edges, $E = 30$
Number of faces, $F = 12$
We need to find $V$.
Substitute the given values into Euler's formula:
$V - 30 + 12 = 2$
... (i)
Simplify the left side of the equation:
$V - 18 = 2$
To find $V$, add 18 to both sides of the equation:
$V = 2 + 18$
Calculate the value of $V$:
$V = 20$
The polyhedron has 20 vertices.
Example 15: The distance between City A and City B on a map is given as 6 cm. If the scale represents 1 cm = 200 km, then find the actual distance between City A and City B.
Answer:
Given:
Distance between City A and City B on the map = $6$ cm.
Scale of the map: $1$ cm on the map represents $200$ km in reality.
To Find:
The actual distance between City A and City B.
Solution:
The scale of the map provides a ratio that relates a distance measured on the map to the corresponding actual distance on the ground.
The given scale is $1$ cm = $200$ km.
This means that every $1$ cm measured on the map corresponds to an actual distance of $200$ km.
The distance between City A and City B on the map is given as $6$ cm.
To find the actual distance, we multiply the distance on the map by the value that $1$ cm represents in reality.
Actual distance = Distance on map $\times$ Value of $1$ cm in reality
Actual distance = $6$ cm $\times$ $200$ km/cm
Actual distance = $6 \times 200$ km
$6 \times 200 = 1200$
Actual distance = $1200$ km
The actual distance between City A and City B is 1200 km.
Example 16: Height of a building is 9 m and this building is represented by 9 cm on a map. What is the scale used for the map?
Answer:
Given:
Actual height of the building = 9 m.
Height of the building on the map = 9 cm.
To Find:
The scale used for the map.
Solution:
The scale of a map is the ratio of a distance on the map to the corresponding actual distance on the ground.
We are given that 9 cm on the map represents an actual distance of 9 m.
First, let's express the actual distance in the same units as the map distance. We convert meters to centimeters.
We know that 1 meter = 100 centimeters.
So, 9 meters = $9 \times 100$ cm = 900 cm.
Now we have the relationship:
9 cm on the map represents 900 cm in reality.
To find the scale as what 1 cm on the map represents, we divide both sides of this relationship by 9.
$\frac{9 \text{ cm}}{9} = \frac{900 \text{ cm}}{9}$
$1 \text{ cm} = 100 \text{ cm}$
Alternatively, since 100 cm equals 1 meter, the scale can also be expressed as:
$1 \text{ cm} = 1 \text{ m}$
The scale used for the map is 1 cm = 1 m or 1:100.
Example 17: The scale on a map is 1 mm : 4 m. Find the distance on the map for an actual distance of 52 m.
Answer:
Given:
Scale of the map: 1 mm represents 4 m.
Actual distance = 52 m.
To Find:
The distance on the map corresponding to the actual distance of 52 m.
Solution:
The scale tells us that:
4 meters in reality are represented by 1 mm on the map.
We want to find the map distance for an actual distance of 52 meters.
From the scale, we can find what 1 meter in reality is represented by on the map:
$4 \text{ m} \iff 1 \text{ mm}$
$\frac{4 \text{ m}}{4} \iff \frac{1 \text{ mm}}{4}$
$1 \text{ m} \iff \frac{1}{4} \text{ mm}$
Now, to find the map distance for 52 meters, we multiply the value for 1 meter by 52:
$52 \text{ m} \iff 52 \times \frac{1}{4} \text{ mm}$
Calculate the product:
$52 \times \frac{1}{4} = \frac{52}{4} = 13$
So, 52 meters in reality are represented by 13 mm on the map.
The distance on the map for an actual distance of 52 m is 13 mm.
Example 18: Application of problem solving strategy
Determine the number of edges, vertices and in the following figure:

Answer:
The given figure is a polyhedron.
It has a hexagonal base and triangular faces meeting at an apex.
This shape is a hexagonal pyramid.
We need to determine the number of vertices, edges, and faces.
Vertices ($V$):
The base is a hexagon, which has 6 vertices.
There is one apex vertex above the base.
Total number of vertices = Vertices in base + Apex vertex
$V = 6 + 1 = 7$
Edges ($E$):
The base is a hexagon, which has 6 edges.
There are edges connecting each vertex of the base to the apex. Since there are 6 base vertices, there are 6 lateral edges.
Total number of edges = Edges in base + Lateral edges
$E = 6 + 6 = 12$
Faces ($F$):
There is one base face, which is a hexagon.
There are lateral faces connecting each edge of the base to the apex. Since there are 6 edges in the base, there are 6 triangular lateral faces.
Total number of faces = Base face + Lateral faces
$F = 1 + 6 = 7$
Summary:
Number of vertices, $V = 7$
Number of edges, $E = 12$
Number of faces, $F = 7$
We can verify Euler's formula ($V - E + F = 2$) for this polyhedron:
$V - E + F = 7 - 12 + 7$
$V - E + F = 14 - 12$
$V - E + F = 2$
The formula holds true.
Exercise
Question 1 to 21 (Multiple Choice Questions)
In each of the questions 1 to 21, out of four options only one is correct. Write the correct answer.
Question 1. Which amongst the following is not a polyhedron?

Answer:
Explanation:
A polyhedron is a three-dimensional solid figure whose surface is made up of a finite number of plane faces that are polygons.
Let's examine the given options:
(A) Cube: A cube is made up of 6 square faces. All faces are polygons. Therefore, a cube is a polyhedron.
(B) Pyramid: A pyramid is made up of a polygonal base and triangular faces that meet at a common vertex. All faces are polygons. Therefore, a pyramid is a polyhedron.
(C) Cone: A cone has a circular base and a curved lateral surface that tapers to a point (apex). It has a curved surface, which is not a polygon. Therefore, a cone is not a polyhedron.
(D) Prism: A prism is made up of two identical and parallel polygonal bases and rectangular faces connecting corresponding sides of the bases. All faces are polygons. Therefore, a prism is a polyhedron.
Based on the definition of a polyhedron, the cone is the figure that does not meet the criteria as it has a curved surface.
The correct option is (C) Cone.
Question 2. Which of the following will not form a polyhedron?
(a) 3 triangles
(b) 2 triangles and 3 parallelogram
(c) 8 triangles
(d) 1 pentagon and 5 triangles
Answer:
Explanation:
A polyhedron is a three-dimensional solid whose surface is composed of a finite number of polygonal faces.
Let's consider each option:
(a) 3 triangles: It is not possible to form a closed three-dimensional figure with just three triangular faces. A tetrahedron, which is the simplest polyhedron, requires a minimum of four triangular faces.
(b) 2 triangles and 3 parallelograms: This combination can form a triangular prism. A triangular prism has two parallel triangular bases and three rectangular (or parallelogram) lateral faces. This is a polyhedron.
(c) 8 triangles: This combination can form an octahedron, which is a polyhedron with 8 triangular faces. It can also form other polyhedra like a pyramid with an octagonal base (which would have 8 triangular faces and 1 octagonal base, total 9 faces). Since it's possible to form a polyhedron, this option is valid for forming one.
(d) 1 pentagon and 5 triangles: This combination can form a pentagonal pyramid. It has a pentagonal base and 5 triangular faces meeting at an apex. This is a polyhedron.
Only option (a) cannot form a polyhedron as a closed three-dimensional shape requires a minimum of four faces.
The correct option is (a) 3 triangles.
Question 3. Which of the following is a regular polyhedron?
(a) Cuboid
(b) Triangular prism
(c) Cube
(d) Square prism
Answer:
Explanation:
A regular polyhedron is a polyhedron whose faces are congruent regular polygons and where the same number of faces meet at each vertex.
Let's examine each option:
(a) Cuboid: A cuboid has rectangular faces. While opposite faces are congruent, not all faces are necessarily congruent to each other (unless it's a cube). Rectangles are regular polygons only if they are squares. If the faces are not all congruent regular polygons, it is not a regular polyhedron.
(b) Triangular prism: A triangular prism has two triangular bases and three parallelogram (usually rectangular) lateral faces. The faces are not all congruent, and they are of different types (triangles and parallelograms). Therefore, it is not a regular polyhedron.
(c) Cube: A cube has six congruent square faces. A square is a regular polygon. At each vertex of a cube, three faces meet, and three edges meet. All faces are congruent regular polygons, and the same number of faces meet at each vertex. Therefore, a cube is a regular polyhedron.
(d) Square prism: A square prism has two square bases and four rectangular lateral faces. Unless the rectangular faces are also squares (making it a cube), the faces are not all congruent or of the same type. Therefore, it is generally not a regular polyhedron.
Among the given options, only the cube satisfies the conditions of a regular polyhedron.
The correct option is (c) Cube.
Question 4. Which of the following is a two Dimensional figure?
(a) Rectangle
(b) Rectangular Prism
(c) Square Pyramid
(d) Square Prism
Answer:
Explanation:
A two-dimensional (2D) figure is a flat shape that has only two dimensions: length and width. It lies entirely in a plane.
A three-dimensional (3D) figure is a solid object that has three dimensions: length, width, and height (or depth). It occupies space.
Let's examine each option:
(a) Rectangle: A rectangle is a flat shape with four straight sides and four right angles. It has length and width, and exists in a plane. Therefore, a rectangle is a two-dimensional figure.
(b) Rectangular Prism: A rectangular prism is a solid shape with six rectangular faces. It has length, width, and height. It occupies space. Therefore, a rectangular prism is a three-dimensional figure.
(c) Square Pyramid: A square pyramid is a solid shape with a square base and four triangular faces that meet at a point. It has length, width, and height. It occupies space. Therefore, a square pyramid is a three-dimensional figure.
(d) Square Prism: A square prism is a solid shape with two square bases and four rectangular lateral faces. It has length, width, and height. It occupies space. Therefore, a square prism is a three-dimensional figure.
Among the given options, only the rectangle is a two-dimensional figure.
The correct option is (a) Rectangle.
Question 5. Which of the following can be the base of a pyramid?
(a) Line segment
(b) Circle
(c) Octagon
(d) Oval
Answer:
Explanation:
A pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. The lateral faces of a pyramid are triangles.
The base of a pyramid must be a polygon.
Let's examine each option to see if it is a polygon:
(a) Line segment: A line segment is a part of a line. It is a 1-dimensional object and not a polygon.
(b) Circle: A circle is a 2-dimensional closed curve. It is not made up of straight line segments, so it is not a polygon. A solid with a circular base and an apex is called a cone, which is not a pyramid (as it's not a polyhedron).
(c) Octagon: An octagon is an 8-sided polygon. A pyramid with an octagonal base is called an octagonal pyramid, and it is a valid type of pyramid.
(d) Oval: An oval is a 2-dimensional closed curve. It is not made up of straight line segments, so it is not a polygon.
Since the base of a pyramid must be a polygon, and an octagon is a polygon, an octagon can be the base of a pyramid.
The correct option is (c) Octagon.
Question 6. Which of the following 3D shapes does not have a vertex?
(a) Pyramid
(b) Prism
(c) Cone
(d) Sphere
Answer:
Explanation:
A vertex (plural: vertices) is a point where edges or faces of a three-dimensional solid meet.
Let's examine the vertices of each given 3D shape:
(a) Pyramid: A pyramid has vertices. For example, a square pyramid has vertices at the corners of its square base and one vertex at the apex where the triangular faces meet.
(b) Prism: A prism has vertices. For example, a triangular prism has vertices at the corners of its triangular bases.
(c) Cone: A cone has one vertex at its apex, where the curved surface meets.
(d) Sphere: A sphere is a perfectly round shape in three-dimensional space. It has a continuous curved surface and no edges or corners where faces meet. Therefore, a sphere does not have any vertices.
Among the given options, only the sphere does not have a vertex.
The correct option is (d) Sphere.
Question 7. Solid having only line segments as its edges is a
(a) Polyhedron
(b) Cone
(c) Cylinder
(d) Polygon
Answer:
Explanation:
Let's examine the edges of the given shapes:
(a) Polyhedron: A polyhedron is a three-dimensional solid bounded by polygonal faces. The intersection of two faces of a polyhedron forms an edge, and these edges are always line segments. Examples of polyhedra include cubes, prisms, and pyramids.
(b) Cone: A cone has a circular base and a curved lateral surface meeting at an apex. It has a single edge where the base meets the curved surface, which is a circle (a curved line), not a line segment.
(c) Cylinder: A cylinder has two parallel circular bases and a curved lateral surface. It has two edges where the bases meet the curved surface, and these are circles (curved lines), not line segments.
(d) Polygon: A polygon is a two-dimensional closed shape made up of line segments. The question asks for a solid (a 3D shape), so this option is incorrect as it is a 2D figure.
The solid shape among the options that has only line segments as its edges is a polyhedron.
The correct option is (a) Polyhedron.
Question 8. In a solid if F = V = 5, then the number of edges in this shape is
(a) 6
(b) 4
(c) 8
(d) 2
Answer:
Explanation:
We are given a solid with the number of faces ($F$) and the number of vertices ($V$). We need to find the number of edges ($E$).
Given:
F = 5
V = 5
We can use Euler's formula for polyhedra, which states the relationship between the number of faces, vertices, and edges:
F + V - E = 2
... (i)
Substitute the given values of $F$ and $V$ into Euler's formula:
5 + 5 - E = 2
Simplify the equation:
10 - E = 2
To find $E$, rearrange the equation:
E = 10 - 2
E = 8
... (ii)
So, the number of edges in this solid shape is 8.
A solid with F=5, V=5, and E=8 is a square pyramid (1 square base + 4 triangular faces = 5 faces; 4 base vertices + 1 apex vertex = 5 vertices; 4 base edges + 4 lateral edges = 8 edges).
The correct option is (c) 8.
Question 9. Which of the following is the top view of the given shape?
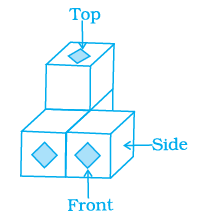

Answer:
Explanation:
We need to determine the shape seen when looking down directly from above the given 3D object.
The given 3D shape consists of two parts:
1. A larger rectangular block at the bottom.
2. A smaller square block placed centrally on top of the rectangular block.
When viewed from the top:
The bottom rectangular block will appear as its base rectangle.
The top square block will appear as its base square.
Since the square block is placed on top of the rectangular block, the top view will show the outline of the rectangular base with the outline of the square top block inside it. This is because the square is within the boundaries of the rectangle when viewed from above.
Therefore, the top view will be a large rectangle with a smaller square drawn inside it.
Now let's look at the given options:
Option (a) shows a single rectangle.
Option (b) shows a rectangle with a square inside it.
Option (c) shows a single square.
Option (d) shows a rectangle divided into smaller rectangles.
Comparing our expected top view with the options, option (b) matches the description of a rectangle with a square inside.
The correct option is (b).
Question 10. The net shown below can be folded into the shape of a cube. The face marked with the letter L is opposite to the face marked with which letter?

(a) M
(b) N
(c) Q
(d) O
Answer:
Explanation:
We are given the net of a cube and asked to find the face opposite to the face marked with the letter L.
When folding a cube net, opposite faces are generally separated by one face in a straight line (either horizontally or vertically).
Let's visualize folding the given net:
The face marked L is in a horizontal strip with faces M, N, O, and P.
Starting from L and moving horizontally:
L is next to M.
M is next to N.
N is next to O.
O is next to P.
In a linear arrangement of faces that form a side or base of the cube, faces that are two steps apart will be opposite to each other when folded.
Looking at the horizontal strip: L, M, N, O, P
L is two steps away from N (L -> M -> N). So, L is opposite to N.
M is two steps away from O (M -> N -> O). So, M is opposite to O.
The face Q is attached to the face N. When the net is folded, Q will become the top or bottom face, and N will be one of the side faces.
Let's confirm using the rule that opposite faces are separated by one face in a line.
In the horizontal strip L-M-N-O-P:
L is opposite to N.
M is opposite to O.
The remaining face P is opposite to the face Q (which is connected to N and will be the other base/top face).
Therefore, the face opposite to the face marked with the letter L is the face marked with the letter N.
The correct option is (b) N.
Question 11. Which of the nets given below will generate a cone?


Answer:
Explanation:
A cone is a three-dimensional geometric shape that tapers smoothly from a flat, circular base to a point called the apex or vertex.
The net of a solid is a two-dimensional shape that can be folded to form the three-dimensional solid.
Let's analyze the nets provided in the images:
Net (a): This net consists of a triangle and a circle. When folded, the triangle will likely form a lateral face, and the circle will form a base. This type of net typically forms a pyramid with a triangular base, not a cone.
Net (b): This net consists of a sector of a circle and a circle. When the sector of a circle is rolled up, the two straight edges meet to form the curved surface of the cone, with the common point becoming the apex. The arc of the sector becomes the circumference of the base. The separate circle in the net forms the base of the cone. This net correctly represents the surface area of a cone and can be folded to form a cone.
Net (c): This net consists of two circles connected by a rectangle. When folded, the rectangle rolls up to form the curved lateral surface, and the two circles form the top and bottom bases. This net forms a cylinder, not a cone.
Net (d): This net consists of a polygon (in this case, a rectangle) and several triangles attached to its sides. When folded, the polygon forms the base, and the triangles form the lateral faces that meet at an apex. This net forms a pyramid with a rectangular base, not a cone.
Based on the structure of a cone and its net, the net that generates a cone is the one composed of a sector of a circle and a circle.
The correct option is (b).
Question 12. Which of the following is not a prism?

Answer:
Explanation:
A prism is a polyhedron consisting of a polygonal base, a translated copy of the base, and faces joining corresponding sides. The lateral faces of a prism are parallelograms (often rectangles in right prisms).
Let's examine each figure:
Figure (a): This shape has two parallel and congruent triangular bases and three rectangular lateral faces connecting the corresponding sides of the bases. This is a triangular prism.
Figure (b): This shape has a rectangular base and four triangular faces meeting at a single point (apex). This shape is a rectangular pyramid. The lateral faces are triangles, not parallelograms, and there is only one base, not two parallel congruent bases.
Figure (c): This shape has two parallel and congruent pentagonal bases and five rectangular lateral faces connecting the corresponding sides of the bases. This is a pentagonal prism.
Figure (d): This shape has two parallel and congruent hexagonal bases and six rectangular lateral faces connecting the corresponding sides of the bases. This is a hexagonal prism.
Based on the definition, a prism must have two parallel and congruent bases and parallelogram lateral faces. Figure (b) is a pyramid, which has only one base and triangular lateral faces.
Therefore, Figure (b) is not a prism.
The correct option is (b).
Question 13. We have 4 congruent equilateral triangles. What do we need more to make a pyramid?
(a) An equilateral triangle.
(b) A square with same side length as of triangle.
(c) 2 equilateral triangles with side length same as triangle.
(d) 2 squares with side length same as triangle.
Answer:
Explanation:
A pyramid is a polyhedron formed by connecting a polygonal base to an apex. The lateral faces of a pyramid are triangles, and the number of lateral faces is equal to the number of sides of the base polygon.
We are given 4 congruent equilateral triangles. These triangles will form the lateral faces of the pyramid.
Since there are 4 lateral faces, the base of the pyramid must be a polygon with 4 sides.
A polygon with 4 sides is a quadrilateral.
Since the 4 triangular faces are congruent and equilateral, the length of their bases (which form the edges of the base polygon) must all be equal. Therefore, the base polygon must be a quadrilateral with all sides equal.
A quadrilateral with all sides equal is either a rhombus or a square.
To form a standard pyramid where the apex is directly above the center of the base (a right pyramid), and given congruent lateral faces, the base is typically a regular polygon. The regular quadrilateral is a square.
For the triangular faces to fit perfectly onto the base, the side length of the square base must be the same as the side length of the equilateral triangles.
Let's examine the options:
(a) An equilateral triangle: A pyramid with a triangular base (a tetrahedron) has 4 faces, all of which are triangles. If the 4 given triangles already form the faces of a tetrahedron, nothing more is needed. However, the question asks what is needed *more*, implying the 4 triangles are just the lateral faces and the base is missing. If the base is a triangle, there would only be 3 lateral faces.
(b) A square with same side length as of triangle: This would provide a 4-sided base. If the side length of the square is the same as the side length of the equilateral triangles, the triangles can be attached to each side of the square to form a square pyramid. This fits the criteria.
(c) 2 equilateral triangles with side length same as triangle: This would result in a total of 6 triangles. This does not form a standard pyramid structure with 4 lateral faces.
(d) 2 squares with side length same as triangle: A pyramid has only one base. Adding two squares would not form a pyramid.
Therefore, to make a pyramid with 4 congruent equilateral triangles as lateral faces, a square with the same side length as the triangle is needed for the base.
The correct option is (b) A square with same side length as of triangle.
Question 14. Side of a square garden is 30 m. If the scale used to draw its picture is 1 cm : 5 m, the perimeter of the square in the picture is
(a) 20 cm
(b) 24 cm
(c) 28 cm
(d) 30 cm
Answer:
Explanation:
We are given the actual side length of a square garden and the scale used to draw its picture. We need to find the perimeter of the square in the picture.
Given:
Actual side length of square garden = 30 m
Scale used for the picture = 1 cm : 5 m
To Find:
The perimeter of the square in the picture.
Solution:
First, we need to determine the side length of the square in the picture using the given scale.
The scale 1 cm : 5 m means that every 5 meters of actual length are represented by 1 centimeter in the picture.
To find the side length in centimeters in the picture, we use the proportion from the scale:
$\frac{\text{Side length in picture (cm)}}{\text{Actual side length (m)}} = \frac{1 \text{ cm}}{5 \text{ m}}$
Rearranging to find the side length in the picture:
$\text{Side length in picture (cm)} = \text{Actual side length (m)} \times \frac{1 \text{ cm}}{5 \text{ m}}$
Substitute the given actual side length (30 m):
$\text{Side length in picture} = 30 \text{ m} \times \frac{1 \text{ cm}}{5 \text{ m}}$
$\text{Side length in picture} = \frac{30}{5} \text{ cm}$
$\text{Side length in picture} = 6 \text{ cm}$
... (i)
Now, we can calculate the perimeter of the square in the picture.
The formula for the perimeter of a square is $P = 4 \times s$, where $s$ is the side length.
$\text{Perimeter in picture} = 4 \times \text{Side length in picture}$
Substitute the side length from (i):
$\text{Perimeter in picture} = 4 \times 6 \text{ cm}$
$\text{Perimeter in picture} = 24 \text{ cm}$
... (ii)
The perimeter of the square garden in the picture is 24 cm.
The correct option is (b) 24 cm.
Question 15. Which of the following shapes has a vertex.

Answer:
Explanation:
A vertex (plural: vertices) is a corner point of a geometric shape. In 3D shapes, it is where edges meet or where a curved surface tapers to a point.
Let's examine each figure:
Figure (a): This figure is a cylinder. A cylinder has two circular bases and a curved lateral surface. It has edges (where the bases meet the curved surface) but no vertices (points where edges meet or where a curved surface tapers to a point).
Figure (b): This figure is a sphere. A sphere is a perfectly round 3D shape with a continuous curved surface. It has no edges or vertices.
Figure (c): This figure is a cone. A cone has a circular base and a curved lateral surface that tapers to a single point called the apex. The apex is a vertex of the cone.
Figure (d): This figure is a torus (like a donut). It is a shape with a continuous curved surface. It has no edges or vertices.
Among the given options, only the cone has a vertex (the apex).
The correct option is (c).
Question 16. In the given map, the distance between the places is shown using the scale 1 cm : 0.5 km. Then the actual distance (in km) between school and the book shop is

(a) 1.25
(b) 2.5
(c) 2
(d) 1.1
Answer:
Explanation:
We are given the scale used in a map and the distance between the school and the book shop on the map. We need to find the actual distance between these two places.
Given:
Scale of the map = 1 cm : 0.5 km
Distance between School and Book Shop on the map = 2.5 cm (from the provided image)
To Find:
The actual distance (in km) between School and the Book Shop.
Solution:
The scale 1 cm : 0.5 km means that every 1 centimeter on the map represents an actual distance of 0.5 kilometers on the ground.
To find the actual distance, we can set up a ratio based on the scale:
$\frac{\text{Actual Distance}}{\text{Distance on Map}} = \frac{0.5 \text{ km}}{1 \text{ cm}}$
We are given the distance on the map (2.5 cm), so we can substitute this value into the equation to find the actual distance:
$\frac{\text{Actual Distance}}{2.5 \text{ cm}} = \frac{0.5 \text{ km}}{1 \text{ cm}}$
Now, we can solve for the Actual Distance:
$\text{Actual Distance} = 2.5 \text{ cm} \times \frac{0.5 \text{ km}}{1 \text{ cm}}$
$\text{Actual Distance} = 2.5 \times 0.5 \text{ km}$
Performing the multiplication:
$\text{Actual Distance} = 1.25 \text{ km}$
... (i)
The actual distance between the School and the Book Shop is 1.25 km.
The correct option is (a) 1.25.
Question 17. Which of the following cannot be true for a polyhedron?
(a) V = 4, F = 4, E = 6
(b) V = 6, F = 8, E = 12
(c) V = 20, F = 12, E = 30
(d) V = 4, F = 6, E = 6
Answer:
Explanation:
For any convex polyhedron (and many non-convex polyhedra), Euler's formula must hold true. Euler's formula is:
F + V - E = 2
... (i)
where $F$ is the number of faces, $V$ is the number of vertices, and $E$ is the number of edges.
We need to check which of the given options does not satisfy Euler's formula.
(a) V = 4, F = 4, E = 6
Substitute into Euler's formula:
F + V - E = 4 + 4 - 6
= 8 - 6
= 2
Since $2 = 2$, this set of values satisfies Euler's formula. This corresponds to a tetrahedron (a triangular pyramid).
(b) V = 6, F = 8, E = 12
Substitute into Euler's formula:
F + V - E = 8 + 6 - 12
= 14 - 12
= 2
Since $2 = 2$, this set of values satisfies Euler's formula. This corresponds to an octahedron.
(c) V = 20, F = 12, E = 30
Substitute into Euler's formula:
F + V - E = 12 + 20 - 30
= 32 - 30
= 2
Since $2 = 2$, this set of values satisfies Euler's formula. This corresponds to a dodecahedron.
(d) V = 4, F = 6, E = 6
Substitute into Euler's formula:
F + V - E = 6 + 4 - 6
= 10 - 6
= 4
Since $4 \neq 2$, this set of values does not satisfy Euler's formula. Therefore, a polyhedron cannot have these numbers of faces, vertices, and edges.
The correct option is (d) V = 4, F = 6, E = 6.
Question 18. In a blueprint of a room, an architect has shown the height of the room as 33 cm. If the actual height of the room is 330 cm, then the scale used by her is
(a) 1 : 11
(b) 1 : 10
(c) 1 : 100
(d) 1 : 3
Answer:
Explanation:
We are given the height of a room in a blueprint and the actual height of the room. We need to determine the scale used in the blueprint.
Given:
Height of the room in the blueprint = 33 cm
Actual height of the room = 330 cm
To Find:
The scale used, in the format 1 : x.
Solution:
The scale of a drawing or blueprint represents the ratio of a length on the drawing to the corresponding actual length. It can be expressed as:
$\text{Scale} = \frac{\text{Length in drawing}}{\text{Actual length}}$
Substitute the given values for the height of the room:
$\text{Scale} = \frac{33 \text{ cm}}{330 \text{ cm}}$
To express the scale in the format 1 : x, we simplify the fraction by dividing both the numerator and the denominator by the numerator (33):
$\text{Scale} = \frac{\cancel{33}^{1} \text{ cm}}{\cancel{330}_{10} \text{ cm}}$
$\text{Scale} = \frac{1}{10}$
... (i)
This ratio can be written as a scale of 1 : 10.
This means that 1 cm on the blueprint represents an actual distance of 10 cm in the room.
The scale used by the architect is 1 : 10.
The correct option is (b) 1 : 10.
Question 19. The following is the map of a town. Based on it answer question 19-21.

The number of hospitals in the town is
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
Explanation:
We need to find the number of hospitals in the town based on the provided map.
To do this, we should look at the map and its legend to identify how hospitals are represented.
In the legend shown on the map, there is an entry for "HOSPITAL". The symbol used for the hospital is a red cross within a square.
Now, we need to scan the map to find instances of this symbol or the label "HOSPITAL".
Upon examining the map, we can locate the label "HOSPITAL" in one place.
Counting the number of times "HOSPITAL" is marked on the map, we find there is only 1 hospital.
Therefore, the number of hospitals in the town is 1.
The correct option is (a) 1.
Question 20. The ratio of the number of general stores and that of the ground is
(a) 1 : 2
(b) 2 : 1
(c) 2 : 3
(d) 3 : 2
Answer:
Explanation:
We need to find the ratio of the number of general stores to the number of grounds in the town, based on the provided map.
First, let's count the number of general stores in the town. Look at the map and the legend for the symbol or label representing a "General Store".
In the legend, "General Store" is represented by a symbol. Let's locate this symbol or the label "General Store" on the map.
Scanning the map, we can find the label "General Store" in two places.
Number of General Stores = 2
Next, let's count the number of grounds in the town. Look at the map and the legend for the symbol or label representing a "Ground".
In the legend, "Ground" is represented by the label "GROUND". Let's locate this label on the map.
Scanning the map, we can find the label "GROUND" in one place.
Number of Grounds = 1
Now, we need to find the ratio of the number of general stores and that of the ground. The ratio is expressed as (Number of General Stores) : (Number of Grounds).
Ratio = 2 : 1
... (i)
The ratio of the number of general stores and that of the ground is 2 : 1.
The correct option is (b) 2 : 1.
Question 21. According to the map, the number of schools in the town is
(a) 4
(b) 3
(c) 5
(d) 2
Answer:
Explanation:
We need to find the number of schools in the town based on the provided map.
To do this, we should look at the map and its legend to identify how schools are represented.
In the legend shown on the map (referencing the image from Question 19 which is used for questions 19-21), there is an entry for "SCHOOL". The symbol used for the school is a building with a flag on top.
Now, we need to scan the map to find instances of this symbol or the label "SCHOOL".
Upon examining the map carefully, we can locate the label and symbol for "SCHOOL" in the following places:
- Near the top-left area of the map.
- In the middle-left area of the map.
- In the bottom-right area of the map.
Counting the number of times "SCHOOL" is marked on the map, we find there are 3 schools.
Therefore, according to the map, the number of schools in the town is 3.
The correct option is (b) 3.
Question 22 to 41 (Fill in the Blanks)
In questions 22 to 41, fill in the blanks to make the statements true.
Question 22. Square prism is also called a _______.
Answer:
Explanation:
A square prism is a prism with a square base. Its faces are two congruent square bases and four rectangular lateral faces. If the rectangular lateral faces are also squares (meaning the height of the prism is equal to the side length of the square base), then all six faces are squares.
A solid shape with six congruent square faces is known as a cube.
Therefore, a square prism where the height equals the side of the square base is also called a cube.
The blank should be filled with the word "cube".
Answer: Square prism is also called a cube.
Question 23. Rectangular prism is also called a ________.
Answer:
Explanation:
A rectangular prism is a prism that has a rectangular base. It is a three-dimensional solid with six faces, where all the faces are rectangles. The opposite faces are congruent and parallel.
A solid shape bounded by six rectangular faces is also known as a cuboid.
Therefore, a rectangular prism is also called a cuboid.
The blank should be filled with the word "cuboid".
Answer: Rectangular prism is also called a cuboid.
Question 24. In the figure,
 the number of faces meeting at B is ________.
the number of faces meeting at B is ________.
Answer:
Explanation:
The provided image shows a three-dimensional solid, which appears to be a triangular pyramid (tetrahedron).
We need to find the number of faces meeting at the vertex labeled B.
Let's analyze the structure of the triangular pyramid from the image.
The vertices are labeled A, B, C, and D.
The faces are the triangles that form the surface of the solid: $\triangle ABC$, $\triangle ABD$, $\triangle ACD$, and $\triangle BCD$.
We are interested in the vertex B.
Let's identify which faces share the vertex B:
- Face 1: $\triangle ABC$ (This triangle has vertices A, B, and C. So, B is a vertex of this face).
- Face 2: $\triangle ABD$ (This triangle has vertices A, B, and D. So, B is a vertex of this face).
- Face 3: $\triangle BCD$ (This triangle has vertices B, C, and D. So, B is a vertex of this face).
- Face 4: $\triangle ACD$ (This triangle has vertices A, C, and D. It does not have B as a vertex).
Thus, the faces meeting at vertex B are $\triangle ABC$, $\triangle ABD$, and $\triangle BCD$.
Counting these faces, we find that 3 faces meet at vertex B.
The blank should be filled with the number 3.
Answer: In the figure, the number of faces meeting at B is 3.
Question 25. A pyramid on an n sided polygon has ______ faces.
Answer:
Explanation:
A pyramid is a polyhedron formed by connecting a polygonal base to a single point called the apex.
The faces of a pyramid consist of two types:
1. The base: This is the polygon at the bottom. If the base is an n-sided polygon, there is 1 base face.
2. The lateral faces: These are the triangular faces that connect the sides of the base to the apex. Since there are n sides in the base polygon, there will be n triangular lateral faces.
To find the total number of faces, we add the number of base faces and the number of lateral faces:
Total number of faces = Number of base faces + Number of lateral faces
Total number of faces = 1 + n
... (i)
So, a pyramid on an n-sided polygon has $n+1$ faces.
The blank should be filled with the expression $(n+1)$ or "n+1".
Answer: A pyramid on an n sided polygon has n+1 faces.
Question 26. If a solid shape has 12 faces and 20 vertices, then the number of edges in this solid is ______.
Answer:
Explanation:
We are given the number of faces ($F$) and the number of vertices ($V$) of a solid shape. We need to find the number of edges ($E$).
Given:
Number of faces, F = 12
Number of vertices, V = 20
To Find:
The number of edges, E.
Solution:
Assuming the solid shape is a polyhedron (for which the question is applicable), we can use Euler's formula:
F + V - E = 2
... (i)
Substitute the given values of $F$ and $V$ into Euler's formula:
12 + 20 - E = 2
Simplify the equation:
32 - E = 2
To find $E$, rearrange the equation:
E = 32 - 2
E = 30
... (ii)
So, the number of edges in this solid is 30.
This solid is an icosahedron, a regular polyhedron with 20 triangular faces, 12 vertices, and 30 edges.
The blank should be filled with the number 30.
Answer: If a solid shape has 12 faces and 20 vertices, then the number of edges in this solid is 30.
Question 27. The given net
 can be folded to make a ______.
can be folded to make a ______.
Answer:
Explanation:
The given net consists of a rectangle and two congruent circles attached to opposite sides of the rectangle.
Let's consider how this net folds into a 3D shape:
- The rectangle will form the curved lateral surface of the solid. When the rectangle is rolled up, its width becomes the height of the solid, and its length becomes the circumference of the bases.
- The two circles, attached to the sides corresponding to the length of the rectangle, will form the top and bottom bases of the solid. Since they are circles, the bases will be circular.
A three-dimensional solid with two parallel and congruent circular bases connected by a curved lateral surface is called a cylinder.
Therefore, the given net can be folded to make a cylinder.
The blank should be filled with the word "cylinder".
Answer: The given net can be folded to make a cylinder.
Question 28. A solid figure with only 1 vertex is a ______.
Answer:
Explanation:
We are looking for a solid figure that has exactly one vertex.
Let's consider some common solid shapes and their number of vertices:
- Cube: 8 vertices
- Cuboid: 8 vertices
- Triangular Prism: 6 vertices
- Square Pyramid: 5 vertices (4 at the base, 1 at the apex)
- Triangular Pyramid (Tetrahedron): 4 vertices
- Cylinder: 0 vertices (edges are circles, no sharp corners)
- Sphere: 0 vertices (continuous curved surface)
- Cone: 1 vertex (the apex where the curved surface meets)
From this list, the cone is a solid figure that has only one vertex.
A cone tapers from a base to a single point (the apex), which is its only vertex.
The blank should be filled with the word "cone".
Answer: A solid figure with only 1 vertex is a cone.
Question 29. Total number of faces in a pyramid which has eight edges is______.
Answer:
Explanation:
We are given that a pyramid has eight edges. We need to find the total number of faces in this pyramid.
Let the base of the pyramid be a polygon with $n$ sides.
In a pyramid, the edges consist of the edges of the base polygon and the lateral edges connecting each vertex of the base to the apex.
- Number of edges in the base = $n$
- Number of lateral edges = $n$ (one for each vertex of the base)
The total number of edges ($E$) in a pyramid is the sum of the base edges and the lateral edges:
E = n + n = 2n
... (i)
We are given that the number of edges is 8. So, we have:
2n = 8
... (ii)
Solving for $n$:
n = $\frac{8}{2}$
n = 4
... (iii)
So, the base of the pyramid is a 4-sided polygon (a quadrilateral, likely a square for a standard pyramid).
Now, let's find the number of faces ($F$) in this pyramid.
The faces of a pyramid consist of the base face and the lateral triangular faces.
- Number of base faces = 1 (the n-sided polygon)
- Number of lateral faces = n (one triangular face for each side of the base)
The total number of faces is the sum of the base face and the lateral faces:
F = 1 + n
... (iv)
Substitute the value of $n=4$ from (iii) into (iv):
F = 1 + 4
F = 5
... (v)
So, a pyramid with eight edges has 5 faces.
This corresponds to a square pyramid, which has 1 square base and 4 triangular faces ($1+4=5$ faces), 4 base vertices + 1 apex vertex = 5 vertices, and 4 base edges + 4 lateral edges = 8 edges. Let's check Euler's formula for this: F + V - E = 5 + 5 - 8 = 10 - 8 = 2. The formula holds.
The blank should be filled with the number 5.
Answer: Total number of faces in a pyramid which has eight edges is 5.
Question 30. The net of a rectangular prism has ______ rectangles.
(Hint: Every square is a rectangle but every rectangle is not a square.)
Answer:
Explanation:
A rectangular prism is a polyhedron with six faces. All six faces of a rectangular prism are rectangles. Some or all of these rectangles might also be squares, but since a square is a specific type of rectangle, we can say that all faces are rectangles.
Let's count the number of faces in a rectangular prism.
A rectangular prism has three pairs of congruent and parallel rectangular faces:
- The top and bottom bases (rectangles).
- The front and back faces (rectangles).
- The left and right faces (rectangles).
In total, there are $2 + 2 + 2 = 6$ faces.
Since every face of a rectangular prism is a rectangle, the net of a rectangular prism will consist of the shapes of these six faces laid out in a connected pattern in a plane.
Therefore, the net of a rectangular prism has 6 rectangles.
The hint reminds us that if some of the faces are squares, they are still considered rectangles for the purpose of counting the total number of rectangular faces.
The blank should be filled with the number 6.
Answer: The net of a rectangular prism has 6 rectangles.
Question 31. In a three-dimensional shape, diagonal is a line segment that joins two vertices that do not lie on the ______ face.
Answer:
Explanation:
In geometry, a diagonal connects two non-adjacent vertices. In a three-dimensional shape (a solid), there are two types of diagonals:
1. Face diagonal: A line segment connecting two vertices that lie on the same face but are not adjacent (i.e., they are opposite vertices of that face). These diagonals lie within a single face.
2. Space diagonal (or interior diagonal): A line segment connecting two vertices that do not lie on the same face. These diagonals pass through the interior of the solid.
The statement "In a three-dimensional shape, diagonal is a line segment that joins two vertices that do not lie on the ______ face" describes a space diagonal.
The vertices joined by a space diagonal belong to different faces, specifically faces that are not adjacent or share a common edge.
The vertices do not lie on the **same** face.
The blank should be filled with the word "same".
Answer: In a three-dimensional shape, diagonal is a line segment that joins two vertices that do not lie on the same face.
Question 32. If 4 km on a map is represented by 1 cm, then 16 km is represented by ______ cm.
Answer:
Explanation:
We are given a scale where 4 km on a map is represented by 1 cm. We need to find out how many centimeters represent 16 km on this map.
Given:
Scale: 4 km on map = 1 cm
To Find:
The representation in cm for 16 km.
Solution:
The scale can be expressed as a ratio:
$\frac{\text{Distance on Map (cm)}}{\text{Actual Distance (km)}} = \frac{1 \text{ cm}}{4 \text{ km}}$
We want to find the distance on the map for an actual distance of 16 km. Let the distance on the map be $x$ cm.
$\frac{x \text{ cm}}{16 \text{ km}} = \frac{1 \text{ cm}}{4 \text{ km}}$
... (i)
To solve for $x$, we can cross-multiply or multiply both sides by 16 km:
$x \text{ cm} = 16 \text{ km} \times \frac{1 \text{ cm}}{4 \text{ km}}$
$x = \frac{16}{4}$
$x = 4$
... (ii)
So, 16 km is represented by 4 cm on the map.
The blank should be filled with the number 4.
Answer: If 4 km on a map is represented by 1 cm, then 16 km is represented by 4 cm.
Question 33. If actual distance between two places A and B is 110 km and it is represented on a map by 25 mm. Then the scale used is ______.
Answer:
Explanation:
We are given the actual distance between two places and the distance representing it on a map. We need to find the scale used for the map.
Given:
Actual distance = 110 km
Distance on map = 25 mm
To Find:
The scale used, typically expressed in the format 1 : x (unitless ratio) or 1 unit : y units.
Solution:
The scale is the ratio of the distance on the map to the actual distance.
$\text{Scale} = \frac{\text{Distance on map}}{\text{Actual distance}}$
We need to express both distances in the same unit. Let's convert kilometers to millimeters.
We know that:
1 km = 1000 meters
... (i)
1 meter = 100 centimeters
... (ii)
1 centimeter = 10 millimeters
... (iii)
Combining these conversions:
1 km = 1000 $\times$ 100 $\times$ 10 millimeters
1 km = 1,000,000 mm
... (iv)
Now, convert the actual distance from km to mm:
Actual distance = 110 km = 110 $\times$ 1,000,000 mm
Actual distance = 110,000,000 mm
... (v)
Now, calculate the ratio of map distance to actual distance:
$\text{Scale} = \frac{25 \text{ mm}}{110,000,000 \text{ mm}}$
Simplify the fraction to express the scale in the format 1 : x. Divide both numerator and denominator by 25:
$\text{Scale} = \frac{25 \div 25}{110,000,000 \div 25}$
Let's perform the division $110,000,000 \div 25$:
$110,000,000 \div 25 = (1100 \times 100000) \div 25 = (1100 \div 25) \times 100000$
$1100 \div 25 = 44$
So, $110,000,000 \div 25 = 44 \times 100000 = 4,400,000$
$\text{Scale} = \frac{1}{4,400,000}$
... (vi)
The scale is 1 : 4,400,000.
The blank should be filled with the scale 1 : 4,400,000.
Answer: If actual distance between two places A and B is 110 km and it is represented on a map by 25 mm. Then the scale used is 1 : 4,400,000.
Question 34. A pentagonal prism has ______ faces.
Answer:
Explanation:
A pentagonal prism is a prism with a pentagonal base.
The faces of a prism consist of two types:
1. The bases: There are two congruent and parallel polygonal bases. Since the base is a pentagon, there are 2 pentagonal faces.
2. The lateral faces: These are the faces that connect the corresponding sides of the two bases. In a prism, the lateral faces are parallelograms (usually rectangles in a right prism). The number of lateral faces is equal to the number of sides of the base polygon. Since the base is a pentagon (a 5-sided polygon), there are 5 lateral faces.
To find the total number of faces ($F$) in a pentagonal prism, we add the number of base faces and the number of lateral faces:
F = Number of base faces + Number of lateral faces
F = 2 + 5
F = 7
... (i)
So, a pentagonal prism has 7 faces.
Let's verify using Euler's formula: F + V - E = 2.
Vertices ($V$): A pentagon has 5 vertices. Since there are two bases, the total number of vertices is $5 \times 2 = 10$.
Edges ($E$): A pentagonal base has 5 edges. There are 2 bases, contributing $5 \times 2 = 10$ edges. There are also 5 lateral edges connecting the corresponding vertices of the bases. Total edges = $10 + 5 = 15$.
Check Euler's formula: F + V - E = 7 + 10 - 15 = 17 - 15 = 2. The formula holds, confirming our face count.
The blank should be filled with the number 7.
Answer: A pentagonal prism has 7 faces.
Question 35. If a pyramid has a hexagonal base, then the number of vertices is ______.
Answer:
Explanation:
We are considering a pyramid with a hexagonal base. We need to find the number of vertices in this pyramid.
The vertices of a pyramid consist of two types:
1. The vertices of the base polygon. Since the base is a hexagon, and a hexagon is a 6-sided polygon, it has 6 vertices.
2. The apex: This is the single vertex at the top where all the lateral faces meet.
To find the total number of vertices ($V$) in a hexagonal pyramid, we add the number of vertices in the base and the apex vertex:
V = Number of vertices in base + Number of apex vertices
V = 6 + 1
V = 7
... (i)
So, a pyramid with a hexagonal base has 7 vertices.
The blank should be filled with the number 7.
Answer: If a pyramid has a hexagonal base, then the number of vertices is 7.
Question 36.
 is the _______ view of
is the _______ view of
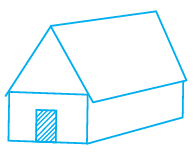
Answer:
The first image shows a rectangle.
The second image shows a 3D object which looks like a house with a rectangular base and a triangular prism on top.
When looking at the second object from the top, we only see the rectangular base.
Therefore, the first image is the top view of the second image.
The blank should be filled with top.
Question 37. The number of cubes in  are ______.
are ______.
Answer:
Let's count the number of cubes layer by layer, starting from the bottom.
The bottom layer appears to be a $2 \times 2$ square arrangement of cubes.
Number of cubes in the bottom layer = $2 \times 2 = 4$.
The second layer from the bottom appears to have 2 cubes arranged in a $2 \times 1$ row on top of part of the bottom layer.
Number of cubes in the second layer = $2 \times 1 = 2$.
The top layer appears to have 1 cube on top of part of the second layer.
Number of cubes in the top layer = $1$.
Total number of cubes = (Cubes in bottom layer) + (Cubes in second layer) + (Cubes in top layer)
Total number of cubes = $4 + 2 + 1 = 7$.
The blank should be filled with 7.
Question 38. If the sum of number of vertices and faces in a polyhedron is 14, then the number of edges in that shape is ______.
Answer:
Let V be the number of vertices, F be the number of faces, and E be the number of edges in a polyhedron.
We are given that the sum of the number of vertices and faces is 14.
V + F = 14
... (i)
According to Euler's formula for convex polyhedrons, the relationship between the number of vertices, faces, and edges is:
V - E + F = 2
[Euler's Formula] ... (ii)
We can rewrite Euler's formula as:
(V + F) - E = 2
Now, substitute the value of (V + F) from equation (i) into this rearranged formula:
$14 - \text{E} = 2$
To find the number of edges E, rearrange the equation:
$\text{E} = 14 - 2$
$\text{E} = 12$
So, the number of edges in the polyhedron is 12.
The blank should be filled with 12.
Question 39. Total number of regular polyhedra is ______.
Answer:
A regular polyhedron is a convex polyhedron where all faces are congruent regular polygons and the same number of faces meet at each vertex.
These are also known as Platonic solids.
There are exactly five convex regular polyhedra:
- The tetrahedron (4 faces, equilateral triangles)
- The cube (6 faces, squares)
- The octahedron (8 faces, equilateral triangles)
- The dodecahedron (12 faces, regular pentagons)
- The icosahedron (20 faces, equilateral triangles)
Thus, the total number of regular polyhedra is 5.
The blank should be filled with 5.
Question 40. A regular polyhedron is a solid made up of ______ faces.
Answer:
A regular polyhedron is a convex polyhedron that is highly symmetrical. By definition, all its faces are identical (congruent) and are regular polygons.
A regular polygon is a polygon that is both equiangular (all angles are equal) and equilateral (all sides are equal).
For example, the faces of a cube are congruent squares (regular polygons), and the faces of a regular tetrahedron are congruent equilateral triangles (regular polygons).
Therefore, a regular polyhedron is a solid made up of faces that are congruent regular polygons.
The blank should be filled with congruent regular polygonal.
Question 41. For each of the following solids, identify the front, side and top views and write it in the space provided.
(a)


(b)


(c)

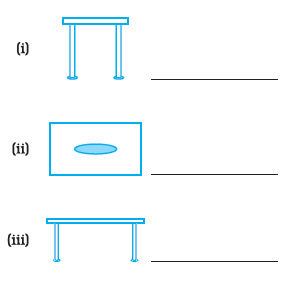
(d)


Answer:
For solid (a) (image 23.png):
The views are shown in image 24.png (Left, Middle, Right).
Front View: The right image in 24.png (Stack of 3 rectangles).
Side View: The middle image in 24.png (L-shape).
Top View: The left image in 24.png (Rectangle).
For solid (b) (image 25.png):
The views are shown in image 26.png (Left, Middle, Right).
Front View: The middle image in 26.png (Stepped shape).
Side View: The left image in 26.png (Rectangle).
Top View: The right image in 26.png (Stepped shape).
For solid (c) (image 27.png):
The views are shown in image 28.png (Left, Middle, Right).
Front View: The middle image in 28.png (Two side-by-side rectangles of different heights).
Side View: The right image in 28.png (Single rectangle).
Top View: The left image in 28.png (Single rectangle).
For solid (d) (image 29.png):
The views are shown in image 30.png (Left, Middle, Right).
Front View: The middle image in 30.png (Stack of 2 rectangles).
Side View: The right image in 30.png (Single rectangle).
Top View: The left image in 30.png (L-shape).
Question 42 to 61 (True or False)
In each of the questions 42 to 61, state whether the following statements are true (T) or false (F).
Question 42. The other name of cuboid is tetrahedron.
Answer:
False
A cuboid is a three-dimensional solid with six rectangular faces. It is also known as a rectangular prism.
A tetrahedron is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. It is the simplest of all the convex polyhedra.
Since a cuboid has 6 faces and a tetrahedron has 4 faces, they are different shapes and one is not another name for the other.
Question 43. A polyhedron can have 3 faces.
Answer:
False
A polyhedron is a three-dimensional solid whose surface is made up of a finite number of polygonal faces. The smallest possible number of faces a polyhedron can have is 4.
The simplest polyhedron is the tetrahedron, which has 4 triangular faces, 6 edges, and 4 vertices.
According to Euler's formula for convex polyhedra, the number of vertices ($V$), edges ($E$), and faces ($F$) are related by the equation:
$V - E + F = 2$
... (i)
Each edge of a polyhedron is shared by exactly two faces. This means that twice the number of edges is equal to the sum of the number of edges of all faces. Since the minimum number of edges for any face is 3 (as faces are polygons), we have:
$2E \geq 3F$
If a polyhedron had 3 faces ($F=3$), then from the inequality $2E \geq 3F$, we would get $2E \geq 3(3) = 9$, which means $E \geq 4.5$. Since the number of edges must be an integer, the minimum number of edges would be $E = 5$.
Now, substituting $F=3$ and $E=5$ into Euler's formula $V - E + F = 2$:
$V - 5 + 3 = 2$
$V - 2 = 2$
$V = 4$
So, if a polyhedron had 3 faces, it would require 5 edges and 4 vertices. However, it is not possible to form a closed three-dimensional figure (a polyhedron) with only 4 vertices and 5 edges where each face is a polygon and each edge is shared by exactly two faces. The minimum number of edges connecting 4 vertices to form a polyhedron is 6 (as in a tetrahedron).
Therefore, a polyhedron must have at least 4 faces.
Question 44. A polyhedron with least number of faces is known as a triangular pyramid.
Answer:
True
As discussed in the previous question, the minimum number of faces a polyhedron can have is 4.
A polyhedron with 4 faces is called a tetrahedron.
A triangular pyramid is a pyramid with a triangle as its base. It has 1 triangular base and 3 triangular lateral faces. Therefore, a triangular pyramid has a total of $1 + 3 = 4$ faces.
A tetrahedron is the same geometric shape as a triangular pyramid. Both are polyhedra with the minimum possible number of faces (4).
Question 45. Regular octahedron has 8 congruent faces which are isosceles triangles.
Answer:
True
A regular octahedron is one of the five Platonic solids. It is a polyhedron with 8 faces, 12 edges, and 6 vertices.
The faces of a regular octahedron are 8 congruent equilateral triangles.
An isosceles triangle is a triangle that has at least two sides of equal length. An equilateral triangle is a triangle in which all three sides are equal in length. Since an equilateral triangle has all three sides equal, it also has at least two sides equal, meaning every equilateral triangle is also an isosceles triangle.
Therefore, since the faces of a regular octahedron are congruent equilateral triangles, they are also congruent isosceles triangles. The statement is true.
Question 46. Pentagonal prism has 5 pentagons.
Answer:
False
A prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases.
A pentagonal prism is a prism with a pentagonal base. This means it has two congruent and parallel pentagonal faces (the bases).
The faces connecting the two pentagonal bases are called lateral faces. Since a pentagon has 5 sides, there are 5 lateral faces, which are rectangles (or parallelograms in a non-right prism).
So, a pentagonal prism has:
- 2 pentagonal faces (the bases)
- 5 rectangular faces (the lateral faces)
The total number of faces is $2 + 5 = 7$.
The statement claims that a pentagonal prism has 5 pentagons, which is incorrect. It has only 2 pentagons.
Question 47. Every cylinder has 2 opposite faces as congruent circles, so it is also a prism.
Answer:
False
A cylinder is a three-dimensional solid with two congruent and parallel circular bases and a curved lateral surface.
A prism is a polyhedron whose bases are two parallel and congruent polygons and whose lateral faces are parallelograms.
While a cylinder shares the property of having two opposite congruent and parallel bases with a prism, the key difference lies in the lateral surface. A prism's lateral surface is composed of flat polygonal faces, whereas a cylinder's lateral surface is curved.
A prism is a type of polyhedron, which means all its faces must be polygons (flat surfaces with straight edges). A cylinder is not a polyhedron because it has a curved surface.
Therefore, despite having congruent circular bases, a cylinder is not classified as a prism.
Question 48. Euler’s formula is true for all three-dimensional shapes.
Answer:
False
Euler's formula relates the number of vertices ($V$), edges ($E$), and faces ($F$) of certain three-dimensional shapes. The formula is:
$V - E + F = 2$
This formula is specifically true for convex polyhedra (three-dimensional solids whose faces are polygons) and some non-convex polyhedra that are topologically equivalent to a sphere.
However, there are many three-dimensional shapes for which this formula does not apply, such as:
- Shapes with curved surfaces (like spheres, cylinders, cones). These shapes do not have distinct vertices, edges, and faces in the way polyhedra do.
- Polyhedra with holes (like a torus or a hollow cube). For these shapes, the formula becomes $V - E + F = 2 - 2g$, where $g$ is the number of "holes" (genus).
Since Euler's formula ($V - E + F = 2$) is not applicable to all three-dimensional shapes (e.g., shapes with curved surfaces), the statement that it is true for all three-dimensional shapes is false.
Question 49. A polyhedron can have 10 faces, 20 edges and 15 vertices.
Answer:
False
For any simple polyhedron (one without holes), the relationship between the number of vertices ($V$), edges ($E$), and faces ($F$) is given by Euler's formula:
$V - E + F = 2$
In the given statement, we have:
$F = 10$ (Number of faces)
$E = 20$ (Number of edges)
$V = 15$ (Number of vertices)
Let's substitute these values into Euler's formula:
$V - E + F = 15 - 20 + 10$
$= -5 + 10$
$= 5$
According to Euler's formula for simple polyhedra, the result must be 2 ($V - E + F = 2$). In this case, we got 5, which is not equal to 2.
This set of values for $V$, $E$, and $F$ does not satisfy Euler's formula for a simple polyhedron, nor for a polyhedron with a non-negative integer number of holes ($V - E + F = 2 - 2g$, where $g$ is the number of holes, requires $5 = 2 - 2g$, which gives $g = -3/2$, not a valid number of holes).
Therefore, a polyhedron cannot have 10 faces, 20 edges, and 15 vertices.
Question 50. The top view of
 is
is

Answer:
True
The top view of an object is what you see when you look at it from directly above.
The first image shows a three-dimensional structure likely made of unit cubes. It appears to have a base layer that forms a rectangle, and additional cubes stacked on top.
Assuming the base layer is a $3 \times 2$ arrangement of cubes and the additional cubes are placed on top within the boundaries of this base, when viewed from directly above, the shape visible will be the outline of the base layer.
The visible area from the top will be a solid rectangle corresponding to the dimensions of the base layer.
The second image is a simple rectangle. If the base of the structure in the first image is rectangular, then its top view will be a rectangle.
Based on the typical representation of such structures with unit cubes, the base is rectangular (likely $3 \times 2$). The top view of such a structure is indeed a rectangle of the same dimensions as the base.
Question 51. The number of edges in a parallelogram is 4.
Answer:
False
A parallelogram is a plane figure (a two-dimensional shape) with four straight sides where opposite sides are parallel and equal in length.
In geometry, the term edges typically refers to the line segments where two faces of a three-dimensional object meet.
Two-dimensional shapes like parallelograms have sides, not edges. A parallelogram has 4 sides.
While the boundaries of a 2D shape can sometimes be referred to loosely as edges in certain contexts (like computer graphics), in formal geometric terms, "edge" is a property of 3D objects (polyhedra, etc.). Since a parallelogram is a 2D shape, it does not have edges in the same way a cube or a prism does.
Therefore, the statement is false because a parallelogram has 4 sides, not 4 edges (in the context of 3D geometry).
Question 52. Every solid shape has a unique net.
Answer:
False
A net is a two-dimensional pattern that can be folded to form a three-dimensional solid shape.
Many solid shapes can be formed by folding different net patterns. This means that a single solid shape often has multiple possible nets, not just one unique net.
For example, a cube (a common solid shape) can be unfolded into several different 2D patterns. There are exactly 11 distinct nets that can be folded to form a cube.
Since solid shapes like the cube have more than one net, the statement that every solid shape has a unique net is false.
Question 53. Pyramids do not have a diagonal.
Answer:
False
In geometry, a diagonal is a line segment joining two non-adjacent vertices of a polygon or a polyhedron.
For a pyramid, we consider diagonals on its faces and potentially space diagonals.
The faces of a pyramid consist of a base polygon and triangular lateral faces. The triangular lateral faces do not have diagonals, as a triangle has no non-adjacent vertices.
The base of a pyramid is a polygon. If the base polygon has 4 or more sides (e.g., a square, a pentagon, a hexagon, etc.), it will have diagonals. For example, a square base has two diagonals connecting opposite corners on the base.
Pyramids generally do not have space diagonals (connecting two vertices that do not lie on the same face), as any line segment connecting the apex to a base vertex is an edge, and any line segment connecting two base vertices is either a base edge or a base diagonal.
Since a pyramid with a base of 4 or more sides has diagonals on its base face, the statement "Pyramids do not have a diagonal" is false.
Question 54. The given shape is a cylinder.
Answer:
I am unable to provide a definitive answer to this question.
The question refers to a "given shape", but the image or description of this shape is not included in the input provided.
To determine if the statement "The given shape is a cylinder" is true or false, I need to see the specific shape being referred to.
A cylinder is a three-dimensional solid with two congruent and parallel circular bases and a curved lateral surface.
Please provide the image or a description of the shape so I can answer the question correctly.
Question 55. A cuboid has atleast 4 diagonals.
Answer:
True
A cuboid is a three-dimensional solid with six rectangular faces.
In a cuboid, we typically consider two types of diagonals:
- Face diagonals: These lie on the faces and connect two non-adjacent vertices on the same face.
- Space diagonals: These pass through the interior of the cuboid and connect two vertices that do not lie on the same face.
Let's consider the space diagonals of a cuboid. A cuboid has 8 vertices. A space diagonal connects a vertex to the opposite vertex that is furthest away and not on the same face.
From any one vertex, there is exactly one other vertex that is diagonally opposite through the interior of the cuboid.
Since there are 8 vertices, and each space diagonal connects two vertices, the total number of space diagonals is $\frac{8}{2} = 4$.
Thus, a cuboid has exactly 4 space diagonals. Since 4 is "at least 4", the statement is true.
(For completeness, a cuboid also has 12 face diagonals, 2 on each of the 6 faces. So, in total, a cuboid has $4 + 12 = 16$ diagonals if both types are counted. In either case, it has at least 4 diagonals.)
Question 56. All cubes are prisms.
Answer:
True
A cube is a three-dimensional solid bounded by six congruent square faces, with three meeting at each vertex.
A prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases.
Let's examine if a cube fits the definition of a prism:
- A cube has two opposite faces that are parallel and congruent squares. These can be considered the bases of the prism. A square is a polygon with $n=4$ sides.
- The faces connecting these two square bases are also squares. A square is a type of rectangle, and a rectangle is a type of parallelogram. There are 4 such lateral faces, corresponding to the 4 sides of the square base.
Since a cube has two parallel and congruent polygonal bases (squares) and lateral faces that are parallelograms (squares/rectangles), it fits the definition of a prism. Specifically, a cube is a type of square prism where the height is equal to the side length of the square base.
Therefore, the statement "All cubes are prisms" is true.
Question 57. A cylinder is a 3-D shape having two circular faces of different radii.
Answer:
False
A cylinder is a three-dimensional geometric shape that has two parallel and congruent (identical in size and shape) circular bases connected by a curved lateral surface.
The key property of a cylinder's bases is that they are congruent circles. Congruent circles have the same radius.
The statement claims that a cylinder has two circular faces of different radii, which contradicts the definition of a cylinder.
A 3-D shape with two circular faces of different radii and a curved surface connecting them would typically be a frustum of a cone or a truncated cone, not a standard cylinder.
Question 58. On the basis of the given figure, the length of a rectangle in the net of a cylinder is same as circumference of circles in its net.

Answer:
True
The figure shows the net of a cylinder. The net typically consists of two congruent circles (which form the top and bottom bases of the cylinder) and one rectangle (which forms the curved lateral surface when rolled up).
When the rectangular part of the net is rolled up to form the curved surface of the cylinder, the two opposite edges of the rectangle meet and join the circumferences of the two circular bases.
This means that the length of the rectangle must be exactly equal to the distance around the circular base, which is the circumference of the circle.
If the radius of the circular base is $r$, the circumference of the circle is $2\pi r$. The length of the rectangle in the net is equal to this circumference, i.e., Length $= 2\pi r$. The width of the rectangle is the height of the cylinder, say $h$.
Therefore, the statement that the length of the rectangle in the net of a cylinder is the same as the circumference of the circles in its net is correct.
Question 59. If a length of 100 m is represented on a map by 1 cm, then the actual distance corresponding to 2 cm is 200 m.
Answer:
True
The given scale on the map is that 1 cm represents an actual distance of 100 m.
This can be written as a ratio:
1 cm (on map) : 100 m (actual distance)
To find the actual distance corresponding to 2 cm on the map, we can multiply both sides of the ratio by 2:
$2 \times (1 \text{ cm}) : 2 \times (100 \text{ m})$
2 cm (on map) : 200 m (actual distance)
So, 2 cm on the map represents an actual distance of 200 m.
The statement is consistent with this calculation.
Question 60. The model of a ship shown is of height 3.5 cm. The actual height of the ship is 210 cm if the scale chosen is 1: 60.

Answer:
True
The problem provides the height of the model ship and the scale used to create the model.
Given information:
- Height of the model = 3.5 cm
- Scale = 1:60
The scale 1:60 means that every unit of measurement on the model represents 60 units of the same measurement in reality. In this case, 1 cm on the model represents 60 cm of the actual ship's size.
To find the actual height of the ship, we multiply the model height by the scale factor:
Actual height = Model height $\times$ Scale factor
Actual height = $3.5 \text{ cm} \times 60$
Calculating the product:
$3.5 \times 60 = \frac{35}{10} \times 60 = 35 \times 6$
$35 \times 6 = 210$
So, the actual height of the ship is 210 cm.
The calculated actual height (210 cm) matches the height given in the statement (210 cm).
Therefore, the statement is true.
Question 61. The actual width of a store room is 280 cm. If the scale chosen to make its drawing is 1:7, then the width of the room in the drawing will be 40 cm.
Answer:
True
The problem involves interpreting a map or drawing scale to find an actual dimension.
Given information:
- Actual width of the store room = 280 cm
- Scale of the drawing = 1:7
A scale of 1:7 means that every 1 unit of measurement on the drawing represents 7 units of the same measurement in reality.
Let $W_{drawing}$ be the width of the room in the drawing and $W_{actual}$ be the actual width of the room.
The scale can be written as a ratio:
$\frac{W_{drawing}}{W_{actual}} = \frac{1}{7}$
We are given $W_{actual} = 280 \text{ cm}$. We need to find $W_{drawing}$.
Rearranging the formula:
$W_{drawing} = \frac{1}{7} \times W_{actual}$
$W_{drawing} = \frac{1}{7} \times 280 \text{ cm}$
$W_{drawing} = \frac{280}{7} \text{ cm}$
$W_{drawing} = 40 \text{ cm}$
The calculated width of the room in the drawing is 40 cm, which matches the value given in the statement.
Therefore, the statement is true.
Question 62 to 102
Question 62. Complete the table given below:

Answer:
Answer:
To complete the table, we need to determine the number of faces ($F$), vertices ($V$), and edges ($E$) for each listed solid. We can then verify Euler's formula ($V - E + F = 2$) for simple polyhedra.
Here is the completed table:
| Solid | No. of Faces (F) | No. of Vertices (V) | No. of Edges (E) | V - E + F |
| Cube | 6 | 8 | 12 | 2 |
| Cuboid | 6 | 8 | 12 | 2 |
| Triangular Prism | 5 | 6 | 9 | 2 |
| Square Pyramid | 5 | 5 | 8 | 2 |
| Triangular Pyramid | 4 | 4 | 6 | 2 |
| Hexagonal Pyramid | 7 | 7 | 12 | 2 |
Explanation for the completed values:
- Cube/Cuboid: Have 6 faces (top, bottom, 4 sides), 8 vertices, and 12 edges. $8 - 12 + 6 = 2$.
- Triangular Prism: Has 2 triangular bases, 3 rectangular lateral faces. Total $F = 2 + 3 = 5$. Vertices are at the corners of the bases, $2 \times 3 = 6$. Edges are on the bases ($2 \times 3$) plus vertical edges connecting bases (3). Total $E = 6 + 3 = 9$. $6 - 9 + 5 = 2$.
- Square Pyramid: Has 1 square base, 4 triangular lateral faces. Total $F = 1 + 4 = 5$. Vertices are the 4 base vertices plus 1 apex vertex. Total $V = 4 + 1 = 5$. Edges are the 4 base edges plus 4 edges connecting base vertices to the apex. Total $E = 4 + 4 = 8$. $5 - 8 + 5 = 2$.
- Triangular Pyramid (Tetrahedron): Has 1 triangular base, 3 triangular lateral faces. Total $F = 1 + 3 = 4$. Vertices are the 3 base vertices plus 1 apex vertex. Total $V = 3 + 1 = 4$. Edges are the 3 base edges plus 3 edges connecting base vertices to the apex. Total $E = 3 + 3 = 6$. $4 - 6 + 4 = 2$.
- Hexagonal Pyramid: Has 1 hexagonal base, 6 triangular lateral faces. Total $F = 1 + 6 = 7$. Vertices are the 6 base vertices plus 1 apex vertex. Total $V = 6 + 1 = 7$. Edges are the 6 base edges plus 6 edges connecting base vertices to the apex. Total $E = 6 + 6 = 12$. $7 - 12 + 7 = 2$.
Question 63. How many faces does each of the following solids, have?
(a) Tetrahedron
(b) Hexahedron
(c) Octagonal Pyramid
(d) Octahedron
Answer:
(a) Tetrahedron: A tetrahedron is a polyhedron with 4 triangular faces.
(b) Hexahedron: A hexahedron is a polyhedron with 6 faces. The most common hexahedron is a cube or a cuboid.
(c) Octagonal Pyramid: An octagonal pyramid has an octagon as its base and 8 triangular faces meeting at the apex. It has a total of $1 + 8 = 9$ faces.
(d) Octahedron: An octahedron is a polyhedron with 8 faces. A regular octahedron has 8 triangular faces.
Question 64. Draw a prism with its base as regular hexagon with one of its face facing you. Now draw the top view, front view and side view of this solid.
Answer:
To draw the views of a hexagonal prism with one of its rectangular faces facing you, imagine the prism is standing upright (with its hexagonal bases parallel to the ground) and you are looking directly at one of its rectangular sides.
Here are the descriptions of the top, front, and side views:
Top View:
When you look at the hexagonal prism from directly above, you see the shape of its base. Since the base is a regular hexagon, the top view is a regular hexagon.
Front View:
When you look at the prism from the front, with one rectangular face directly facing you, you see that rectangular face. The front view will be a rectangle. The height of this rectangle is the height of the prism, and the width is the width of one side of the hexagonal base.
Side View:
When you look at the prism from the side (perpendicular to the front view), you see another rectangular face. The side view will also be a rectangle. The height is again the height of the prism, and the width is the width of one side of the hexagonal base (assuming it's a right hexagonal prism and you are looking perpendicular to a face).
Note: In engineering drawings, lines that are hidden from view (like the back edges) are often shown as dashed lines. However, for a simple representation as typically seen at this level, showing only the visible outline is common.
Question 65. How many vertices does each of the following solids have?
(a) Cone
(b) Cylinder
(c) Sphere
(d) Octagonal Pyramid
(e) Tetrahedron
(f) Hexagonal Prism
Answer:
Here is the number of vertices for each solid:
(a) Cone: A cone has 1 vertex (the apex, the point opposite the circular base).
(b) Cylinder: A cylinder has 0 vertices. It has two circular bases and a curved surface, but no sharp corners (vertices).
(c) Sphere: A sphere has 0 vertices. It is a perfectly round three-dimensional object with no corners.
(d) Octagonal Pyramid: An octagonal pyramid has an octagon as its base, which has 8 vertices. It also has an apex vertex at the top. So, it has $8 + 1 = 9$ vertices.
(e) Tetrahedron: A tetrahedron (which is a triangular pyramid) has 3 vertices on its triangular base and 1 apex vertex. So, it has $3 + 1 = 4$ vertices.
(f) Hexagonal Prism: A hexagonal prism has a hexagonal base (with 6 vertices) and a congruent hexagonal top (with 6 vertices). The total number of vertices is $6 + 6 = 12$.
Question 66. How many edges does each of following solids have?
(a) Cone
(b) Cylinder
(c) Sphere
(d) Octagonal Pyramid
(e) Hexagonal Prism
(f) Kaleidoscope
Answer:
Here is the number of edges for each solid:
(a) Cone: A cone has 1 edge (the circular boundary of the base).
(b) Cylinder: A cylinder has 2 edges (the circular boundaries of the two bases).
(c) Sphere: A sphere has 0 edges. It is a completely smooth, curved surface.
(d) Octagonal Pyramid: An octagonal pyramid has 8 edges on its octagonal base and 8 edges connecting the vertices of the base to the apex. Total edges = $8 + 8 = 16$.
(e) Hexagonal Prism: A hexagonal prism has 6 edges on the top hexagonal base, 6 edges on the bottom hexagonal base, and 6 vertical edges connecting the two bases. Total edges = $6 + 6 + 6 = 18$.
(f) Kaleidoscope: The shape of a kaleidoscope is typically a cylindrical tube or a multi-sided prism. If we consider the common cylindrical form as a solid (like a solid cylinder), it has 2 edges (the two circular ends).
Question 67. Look at the shapes given below and state which of these are polyhedra using Euler’s formula.

Answer:
To determine which of the given shapes are polyhedra using Euler's formula, we first need to identify which shapes are polyhedra based on their definition, and then verify if they satisfy Euler's formula ($V - E + F = 2$).
A polyhedron is a three-dimensional solid whose surface is made up entirely of flat polygonal faces. Shapes with curved surfaces are not polyhedra.
Let's examine each shape shown in the figure:
Shape 1: Cube (or Cuboid)
This shape has 6 flat rectangular faces, straight edges, and sharp vertices. Therefore, it is a polyhedron.
For a cube/cuboid:
- Number of Faces ($F$) = 6
- Number of Vertices ($V$) = 8
- Number of Edges ($E$) = 12
Applying Euler's formula: $V - E + F = 8 - 12 + 6 = -4 + 6 = 2$.
Since the shape is a polyhedron and satisfies Euler's formula, it is confirmed as a simple polyhedron.
Shape 2: Cone
This shape has a curved lateral surface and a circular base. Since it has a curved surface, it is not a polyhedron.
Shape 3: Cylinder
This shape has two circular bases and a curved lateral surface. Since it has curved surfaces, it is not a polyhedron.
Shape 4: Sphere
This shape is entirely made of a single curved surface. Since it has a curved surface, it is not a polyhedron.
Shape 5: Rectangular Pyramid
This shape has a flat rectangular base and four flat triangular lateral faces, straight edges, and sharp vertices. Therefore, it is a polyhedron.
For a rectangular pyramid:
- Number of Faces ($F$) = 1 (base) + 4 (lateral) = 5
- Number of Vertices ($V$) = 4 (base) + 1 (apex) = 5
- Number of Edges ($E$) = 4 (base) + 4 (connecting base to apex) = 8
Applying Euler's formula: $V - E + F = 5 - 8 + 5 = -3 + 5 = 2$.
Since the shape is a polyhedron and satisfies Euler's formula, it is confirmed as a simple polyhedron.
Shape 6: Triangular Prism
This shape has two flat triangular bases and three flat rectangular lateral faces, straight edges, and sharp vertices. Therefore, it is a polyhedron.
For a triangular prism:
- Number of Faces ($F$) = 2 (bases) + 3 (lateral) = 5
- Number of Vertices ($V$) = 3 (base 1) + 3 (base 2) = 6
- Number of Edges ($E$) = 3 (base 1) + 3 (base 2) + 3 (connecting bases) = 9
Applying Euler's formula: $V - E + F = 6 - 9 + 5 = -3 + 5 = 2$.
Since the shape is a polyhedron and satisfies Euler's formula, it is confirmed as a simple polyhedron.
Based on the definition of a polyhedron and the application of Euler's formula, the shapes that are polyhedra are:
- Shape 1 (Cube/Cuboid)
- Shape 5 (Rectangular Pyramid)
- Shape 6 (Triangular Prism)
Question 68. Count the number of cubes in the given shapes.

Answer:
We need to count the number of unit cubes that make up each of the given shapes.
Let's examine the first shape:
The first shape appears to be a rectangular block made of stacked unit cubes.
From the view, it looks like there are two layers of cubes.
The base layer appears to be a rectangle formed by $3 \times 3$ cubes.
Number of cubes in the base layer $= 3 \times 3 = 9$.
The second layer also appears to cover the same $3 \times 3$ area on top of the base layer.
Number of cubes in the second layer $= 3 \times 3 = 9$.
Total number of cubes in the first shape $= 9 + 9 = 18$.
Let's examine the second shape:
This shape is a stepped structure.
We can count the cubes by considering the layers from the bottom up, or by counting the number of cubes in each vertical stack visible from the front/side.
Let's count layer by layer from the bottom:
- The bottom layer seems to have a footprint of 3 cubes in the front row, 2 cubes in the middle row behind the front row, and 1 cube in the back row behind the middle row. Total cubes in the bottom layer = $3 + 2 + 1 = 6$.
- The second layer sits on top of some of the cubes in the bottom layer. Based on the edges, it appears to sit on 2 cubes in the front section and 1 cube in the middle section. Total cubes in the second layer = $2 + 1 = 3$.
- The third layer sits on top of one cube in the second layer. Total cubes in the third layer = $1$.
Total number of cubes in the second shape $= 6 + 3 + 1 = 10$.
The number of cubes in each given shape are:
First shape: 18 cubes
Second shape: 10 cubes
Question 69. Draw the front, side and top view of the given shapes.

Answer:
To draw the front, side, and top views of the given shapes made of unit cubes, we imagine looking at the solid from each perspective and drawing what is seen as a 2D shape.
Shape 1:
This shape appears to be a stepped structure, with 3 cubes in the bottom row, 2 in the middle row, and 1 in the top row, potentially offset or stacked.
- Front View: Assuming the front is the side where the cubes step up from left to right. The front view shows a column of 1 unit height on the left, a column of 2 units height in the middle, and a column of 3 units height on the right. This forms a stepped outline.
- Side View: Assuming the side is the right side. Looking from the right, you would see a single column of 3 units height.
- Top View: Looking from directly above, you would see the top faces of the uppermost cubes in each vertical stack. This shape looks like it has a base of 3 cubes in a row. The top view shows three squares in a line.
Shape 2:
This shape also appears to be a stepped structure, potentially arranged in depth.
- Front View: Assuming the front is the side with the lowest step. The front view shows a stack of 1 unit height on the left, a stack of 2 units height in the middle, and a stack of 3 units height on the right. This forms a stepped outline.
- Side View: Assuming the side is the right side. Looking from the right, you would see a stack of 1 unit height in the front, a stack of 2 units height behind it, and a stack of 3 units height behind that. This view shows the increasing height stepping back into the page.
- Top View: Looking from directly above, you would see the top faces of the uppermost cubes. This shape looks like it has 3 cubes arranged one behind the other. The top view shows three squares in a line, representing the highest point in each column from the front.
Question 70. Using Euler’s formula, find the value of unknown x, y, z, p, q, r, in the following table.
| (I) | (II) | (III) | (IV) | (V) | (VI) | |
|---|---|---|---|---|---|---|
| Facts | 7 | y | 9 | p | 6 | 8 |
| Vertices | 10 | 12 | z | 6 | q | 11 |
| Edges | x | 18 | 16 | 12 | 12 | r |
Answer:
We will use Euler's formula, which states that for any simple polyhedron:
$V - E + F = 2$
where $V$ is the number of vertices, $E$ is the number of edges, and $F$ is the number of faces.
For Column (I):
Given: $F = 7$, $V = 10$, $E = x$.
Using Euler's formula:
$V - E + F = 2$
$10 - x + 7 = 2$
$17 - x = 2$
$x = 17 - 2$
$x = 15$
For Column (II):
Given: $F = y$, $V = 12$, $E = 18$.
Using Euler's formula:
$V - E + F = 2$
$12 - 18 + y = 2$
$-6 + y = 2$
$y = 2 + 6$
$y = 8$
For Column (III):
Given: $F = 9$, $V = z$, $E = 16$.
Using Euler's formula:
$V - E + F = 2$
$z - 16 + 9 = 2$
$z - 7 = 2$
$z = 2 + 7$
$z = 9$
For Column (IV):
Given: $F = p$, $V = 6$, $E = 12$.
Using Euler's formula:
$V - E + F = 2$
$6 - 12 + p = 2$
$-6 + p = 2$
$p = 2 + 6$
$p = 8$
For Column (V):
Given: $F = 6$, $V = q$, $E = 12$.
Using Euler's formula:
$V - E + F = 2$
$q - 12 + 6 = 2$
$q - 6 = 2$
$q = 2 + 6$
$q = 8$
For Column (VI):
Given: $F = 8$, $V = 11$, $E = r$.
Using Euler's formula:
$V - E + F = 2$
$11 - r + 8 = 2$
$19 - r = 2$
$r = 19 - 2$
$r = 17$
The values of the unknowns are:
$x = 15$
$y = 8$
$z = 9$
$p = 8$
$q = 8$
$r = 17$
Here is the completed table:
| (I) | (II) | (III) | (IV) | (V) | (VI) | |
|---|---|---|---|---|---|---|
| Faces | 7 | 8 (y) | 9 | 8 (p) | 6 | 8 |
| Vertices | 10 | 12 | 9 (z) | 6 | 8 (q) | 11 |
| Edges | 15 (x) | 18 | 16 | 12 | 12 | 17 (r) |
Question 71. Can a polyhedron have V = F = 9 and E = 16 ? If yes, draw its figure.
Answer:
To determine if a polyhedron can have $V = 9$, $F = 9$, and $E = 16$, we apply Euler's formula for simple polyhedra:
$V - E + F = 2$
Let's substitute the given values into the formula:
$V - E + F = 9 - 16 + 9$
$= -7 + 9$
$= 2$
Since the calculation results in 2, which satisfies Euler's formula, a simple polyhedron with $V=9$, $F=9$, and $E=16$ can exist.
So, the answer is Yes.
Now, let's identify the type of polyhedron that fits these characteristics and describe how to draw it.
Consider a pyramid with an n-sided polygonal base. It has $n+1$ faces (the base plus $n$ triangular lateral faces), $n+1$ vertices (the $n$ base vertices plus the apex), and $2n$ edges ($n$ base edges plus $n$ edges connecting the base vertices to the apex).
If the number of faces $F = 9$, then for a pyramid, $n+1 = 9$, which implies $n=8$. The base is an octagon.
Let's check the number of vertices and edges for an octagonal pyramid (where $n=8$):
- Number of Faces ($F$): $n+1 = 8+1 = 9$
- Number of Vertices ($V$): $n+1 = 8+1 = 9$
- Number of Edges ($E$): $2n = 2 \times 8 = 16$
These values ($V=9$, $F=9$, $E=16$) match the given parameters.
Therefore, the polyhedron is an octagonal pyramid.
Drawing the figure of an Octagonal Pyramid:
To draw an octagonal pyramid:
- Draw a representation of an octagon (a polygon with 8 sides). Since it's a 3D drawing, it should look slightly tilted or flattened when viewed from an angle.
- Choose a point above the approximate center of the octagon. This point represents the apex of the pyramid.
- Draw a straight line segment (representing an edge) from each vertex of the octagon to the apex.
- Use solid lines for the edges that would be visible from your viewpoint and dashed lines for the edges that would be hidden behind the solid faces. Typically, in a standard view, some base edges and some edges connecting base vertices to the apex will be hidden.
Question 72. Check whether a polyhedron can have V = 12, E = 6 and F = 8.
Answer:
To check whether a polyhedron can have $V = 12$, $E = 6$, and $F = 8$, we use Euler's formula for simple polyhedra:
$V - E + F = 2$
Substitute the given values into the formula:
$V - E + F = 12 - 6 + 8$
$= 6 + 8$
$= 14$
According to Euler's formula, for a simple polyhedron, the value of $V - E + F$ must be equal to 2. In this case, the value is 14.
Since $14 \neq 2$, the given number of vertices, edges, and faces does not satisfy Euler's formula for a simple polyhedron.
Also, for any polyhedron, each edge connects exactly two vertices ($2E \geq 3V$) and each edge is shared by exactly two faces ($2E \geq 3F$). With $V=12$ and $E=6$, $2E = 12$, $3V = 36$. $12 \geq 36$ is false. This immediately shows such a polyhedron is impossible.
Therefore, a polyhedron cannot have $V = 12$, $E = 6$, and $F = 8$.
Question 73. A polyhedron has 60 edges and 40 vertices. Find the number of its faces.
Answer:
We are given the number of edges and vertices of a polyhedron and asked to find the number of its faces.
Given information:
- Number of Edges ($E$) = 60
- Number of Vertices ($V$) = 40
- Number of Faces ($F$) = ?
We can use Euler's formula for simple polyhedra, which states:
$V - E + F = 2$
Substitute the given values into the formula:
$40 - 60 + F = 2$
$-20 + F = 2$
Now, solve for $F$:
$F = 2 + 20$
$F = 22$
The number of faces of the polyhedron is 22.
Question 74. Find the number of faces in the given shapes:

Answer:
We need to find the number of faces for each of the given solid shapes.
Let's identify each shape and count its faces:
1. Shape 1: Cube
A cube is a polyhedron with 6 square faces.
Number of faces = 6.
2. Shape 2: Cylinder
A cylinder has two flat circular bases and one curved lateral surface. In terms of surfaces (often referred to as faces in simpler contexts, though not all are flat polygons), it has 2 circular faces and 1 curved face.
Number of faces (surfaces) = 3.
3. Shape 3: Sphere
A sphere has a single continuous curved surface.
Number of faces (surface) = 1.
4. Shape 4: Cone
A cone has one flat circular base and one curved lateral surface. In terms of surfaces, it has 1 circular face and 1 curved face.
Number of faces (surfaces) = 2.
5. Shape 5: Cuboid
A cuboid is a polyhedron with 6 rectangular faces.
Number of faces = 6.
6. Shape 6: Triangular Prism
A triangular prism has two triangular bases and three rectangular lateral faces.
Total number of faces = 2 (triangles) + 3 (rectangles) = 5.
7. Shape 7: Square Pyramid
A square pyramid has one square base and four triangular lateral faces.
Total number of faces = 1 (square) + 4 (triangles) = 5.
Question 75. A polyhedron has 20 faces and 12 vertices. Find the edges of the polyhedron.
Answer:
We are given the number of faces and vertices of a polyhedron and need to find the number of its edges.
Given information:
- Number of Faces ($F$) = 20
- Number of Vertices ($V$) = 12
- Number of Edges ($E$) = ?
We use Euler's formula for simple polyhedra, which states:
$V - E + F = 2$
Substitute the given values into the formula:
$12 - E + 20 = 2$
$32 - E = 2$
Now, solve for $E$:
$E = 32 - 2$
$E = 30$
The number of edges of the polyhedron is 30.
Question 76. A solid has forty faces and, sixty edges. Find the number of vertices of the solid.
Answer:
We are given the number of faces and edges of a solid (which is a polyhedron) and need to find the number of its vertices.
Given information:
- Number of Faces ($F$) = 40
- Number of Edges ($E$) = 60
- Number of Vertices ($V$) = ?
We use Euler's formula for simple polyhedra, which states:
$V - E + F = 2$
Substitute the given values into the formula:
$V - 60 + 40 = 2$
$V - 20 = 2$
Now, solve for $V$:
$V = 2 + 20$
$V = 22$
The number of vertices of the solid is 22.
Question 77. Draw the net of a regular hexahedron with side 3 cm. (Hint: Regular hexahedron - cube)
Answer:
A regular hexahedron is another name for a cube. It is a three-dimensional solid with six congruent square faces.
A net of a solid is a two-dimensional pattern that can be folded along its edges to form the solid shape.
A cube with a side length of 3 cm has six square faces, each with side length 3 cm.
There are several possible nets for a cube. One common net is the "cross" shape. Here is a description of this net:
- Arrange four squares of side 3 cm in a row, connected edge-to-edge.
- Attach one more square of side 3 cm to the top edge of the second square in the row.
- Attach the final square of side 3 cm to the bottom edge of the second square in the row.
Each square in the net has dimensions 3 cm $\times$ 3 cm.
When folded, the four squares in the row form the four sides of the cube, and the two squares attached to the second square form the top and bottom bases.
This is just one of the 11 distinct nets for a cube.
Question 78. Draw the net of a regular tetrahedron with side 6 cm.
Answer:
A regular tetrahedron is a polyhedron with 4 congruent equilateral triangular faces. It is the simplest type of pyramid, with a triangular base and three triangular lateral faces.
A net of a solid is a 2D pattern that can be folded to form the solid.
For a regular tetrahedron with side 6 cm, each of its four faces is an equilateral triangle with side length 6 cm.
The simplest net for a regular tetrahedron consists of four equilateral triangles arranged in a way that they can be folded together.
Drawing the net:
One common way to draw the net of a regular tetrahedron is as follows:
- Draw a central equilateral triangle with each side measuring 6 cm.
- Draw an equilateral triangle with side 6 cm attached to each of the three sides of the central triangle. These three triangles should extend outwards from the central one.
- The resulting shape will be four equilateral triangles connected side-to-side, forming a larger triangle made of four smaller ones.
When the three outer triangles are folded upwards along the edges of the central triangle, their vertices will meet at a single point, forming the apex of the tetrahedron, and their edges will join to form the lateral edges of the solid. The central triangle forms the base.
Each small triangle within this net has sides of length 6 cm.
Question 79. Draw the net of the following cuboid:
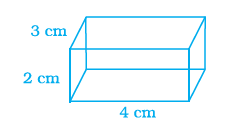
Answer:
The net of a cuboid is a two-dimensional pattern that can be folded to form the cuboid. A cuboid has 6 rectangular faces.
From the given figure, assuming the visible dimensions are Length, Height, and Width (Depth), let's say the dimensions of the cuboid are:
- Length ($l$) = 5 cm
- Height ($h$) = 3 cm
- Width ($w$) = 2 cm
The cuboid has the following six faces with their dimensions:
- Front and Back faces: $l \times h$ (5 cm $\times$ 3 cm)
- Top and Bottom faces: $l \times w$ (5 cm $\times$ 2 cm)
- Left and Right side faces: $w \times h$ (2 cm $\times$ 3 cm)
There are several possible nets for a cuboid. One common net arrangement resembles a cross shape or a "T" shape with extra rectangles.
Description of one possible net:
Imagine placing the Front face ($5 \text{ cm} \times 3 \text{ cm}$) in the center.
Attach the Top face ($5 \text{ cm} \times 2 \text{ cm}$) to the top edge of the Front face (the 5 cm edge).
Attach the Bottom face ($5 \text{ cm} \times 2 \text{ cm}$) to the bottom edge of the Front face (the 5 cm edge).
Attach the Left side face ($2 \text{ cm} \times 3 \text{ cm}$) to the left edge of the Front face (the 3 cm edge).
Attach the Right side face ($2 \text{ cm} \times 3 \text{ cm}$) to the right edge of the Front face (the 3 cm edge).
Finally, attach the Back face ($5 \text{ cm} \times 3 \text{ cm}$) to the top edge of the Top face (the 5 cm edge). Note that the 5 cm edge of the Back face aligns with the 5 cm edge of the Top face.
The layout of the rectangles in this net would be:
[Back face (5 cm $\times$ 3 cm)]
[Top face (5 cm $\times$ 2 cm)]
[Left face (2 cm $\times$ 3 cm)][Front face (5 cm $\times$ 3 cm)][Right face (2 cm $\times$ 3 cm)]
[Bottom face (5 cm $\times$ 2 cm)]
When drawing, ensure the dimensions of adjacent edges that will be joined when folding are the same (e.g., the 5 cm top edge of the Front face matches the 5 cm bottom edge of the Top face).
Question 80. Match the following:
Answer:
Here is the matching of the shapes to their names:
- Shape (i) is a Cone. Match: (i) - (R)
- Shape (ii) is a Cylinder. Match: (ii) - (P)
- Shape (iii) is a Square Pyramid. Match: (iii) - (T)
- Shape (iv) is a Cuboid. Match: (iv) - (S)
- Shape (v) is a Triangular Prism. Match: (v) - (U)
- Shape (vi) is a Cube. Match: (vi) - (Q)
Question 81. Complete the table given below by putting tick mark across the respective property found in the solids mentioned.
| Solids | ||||
|---|---|---|---|---|
| Properties | Cone | Cylinder | Prism | Pyramid |
| 1. The figure is a polyhedron | ||||
| 2. The figure has diagonals | ||||
| 3. The shape has curved edges | ||||
| 4. The base of figure is a polygon. | ||||
| 5. The base are congruent. | ||||
| 6. The base of figure is a polygon and other faces meet at a single point. | ||||
| 7. The base of figure is a curved edge and othe faces meet at a single point. | ||||
Answer:
Here is the completed table indicating which properties apply to each solid:
| Solids | ||||
|---|---|---|---|---|
| Properties | Cone | Cylinder | Prism | Pyramid |
| 1. The figure is a polyhedron | ✓ | ✓ | ||
| 2. The figure has diagonals | ✓ | ✓ | ||
| 3. The shape has curved edges | ✓ | ✓ | ||
| 4. The base of figure is a polygon. | ✓ | ✓ | ||
| 5. The bases are congruent. | ✓ | ✓ | ||
| 6. The base of figure is a polygon and other faces meet at a single point. | ✓ | |||
| 7. The base of figure is a curved edge and other faces meet at a single point. | ✓ | |||
Question 82. Draw the net of the following shape.

Answer:
The given shape is a cone.
The net of a cone consists of two parts:
- The circular base.
- The curved lateral surface, which when unrolled, forms a sector of a circle.
Drawing the net of a cone:
To draw the net, you need:
- A circle representing the base of the cone.
- A sector of a larger circle. The radius of this larger circle is equal to the slant height of the cone. The arc length of this sector is equal to the circumference of the cone's base circle ($2\pi r$, where $r$ is the radius of the base).
Imagine drawing the circular base first. Then, draw a sector of a circle such that its curved edge has the same length as the circumference of the base circle. One radial edge of the sector will attach to a point on the circumference of the base circle. The other radial edge of the sector will join the first when the sector is rolled up to form the cone.
The net is formed by attaching the circular base to the straight edge of the sector.
Question 83. Draw the net of the following solid.

(Hint: Pentagons are not congruent.)
Answer:
The given shape is a frustum of a pentagonal pyramid. It has a larger pentagonal base, a smaller pentagonal top, and five trapezoidal lateral faces connecting the two bases.
The net of this solid will consist of seven faces:
- One large pentagon (the base).
- One small pentagon (the top).
- Five trapezoids (the lateral faces).
To draw the net, imagine unfolding the solid. A common way to lay out the net is to place one of the bases, then arrange the lateral faces around its edges, and finally attach the other base to one of the lateral faces.
Description of one possible net:
- Draw the larger pentagonal base. Let's call this Pentagon 1.
- From each side of Pentagon 1, draw a trapezoidal lateral face outwards. Since there are five sides on the pentagon, you will draw five trapezoids. These trapezoids will be arranged side-by-side around Pentagon 1.
- The edge of each trapezoid that is attached to Pentagon 1 corresponds to a side of the larger pentagon. The opposite, parallel edge of each trapezoid corresponds to a side of the smaller pentagon (Pentagon 2). The lengths of these edges will be different (larger side length for the edge attached to Pentagon 1, smaller side length for the opposite edge).
- Draw the smaller pentagonal top (Pentagon 2). This pentagon should be attached to the edge of one of the trapezoidal lateral faces. The edge you attach it to must correspond to one of the sides of Pentagon 2 when folded. The length of the edge of the trapezoid must match the side length of the smaller pentagon.
The net will look like a large pentagon with five trapezoids attached around its periphery, and a smaller pentagon attached to the top edge of one of those trapezoids.
Remember that the lengths of the sides where faces connect in the net must be equal so they can be joined when folded.
Question 84. Find the number of cubes in the base layer of the following figure.

Answer:
The figure shows a three-dimensional structure built from unit cubes.
The base layer is the bottom-most layer of cubes upon which the rest of the structure is built.
Looking at the figure from an angle that allows us to see the extent of the base, we can count the number of cubes along the length and width of this bottom layer.
From the perspective shown, the base layer appears to be a square arrangement of cubes.
- It extends 3 cubes in one direction (e.g., length).
- It extends 3 cubes in the perpendicular direction (e.g., width).
The base layer is a $3 \times 3$ arrangement of cubes.
The number of cubes in the base layer is the product of the dimensions of this layer:
Number of cubes in base layer = Number of cubes in length $\times$ Number of cubes in width
Number of cubes in base layer = $3 \times 3$
Number of cubes in base layer = $9$
There are 9 cubes in the base layer of the given figure.
Question 85. In the above figure, if only the shaded cubes are visible from the top, draw the base layer.
Answer:
The question asks to draw the base layer of the figure shown in the previous question (Question 84), under the hypothetical condition that only the shaded cubes are visible from the top.
First, let's understand what the base layer of the figure from Question 84 is. Looking at the image in Question 84, the structure is built upon a foundation of unit cubes arranged in a square grid.
The figure shows that the bottom-most layer (the base layer) is a $3 \times 3$ arrangement of cubes.
The condition "if only the shaded cubes are visible from the top" describes the appearance of the solid when viewed from directly above. The shaded cubes in the original figure are the top cubes of the front-most columns. There are 3 such shaded cubes arranged in a row.
However, the question specifically asks us to draw the base layer of the solid, not the top view based on the hypothetical condition. The base layer is the actual bottom-most layer of cubes in the figure.
Regardless of what is visible from the very top of the structure, the base layer of the figure shown in Question 84 is composed of 9 cubes arranged in a $3 \times 3$ grid.
To draw the base layer, we can represent its top view as a 2D grid of squares, where each square represents a cube in the base layer.
Drawing of the base layer:
The base layer consists of 9 cubes arranged in a $3 \times 3$ grid. Representing this as a top-down grid of squares:
This table shows the 3x3 arrangement of cubes that forms the base layer of the solid in Question 84.
Question 86. How many faces, edges and vertices does a pyramid have with n sided polygon as its base?
Answer:
A pyramid with an n-sided polygon as its base has the following characteristics:
Faces:
A pyramid has one base face and triangular lateral faces connecting each side of the base to the apex.
The number of lateral faces is equal to the number of sides of the base polygon, which is $n$.
Number of faces = (Number of base faces) + (Number of lateral faces)
Number of faces = $1 + n$
Thus, a pyramid with an n-sided base has $\mathbf{n+1}$ faces.
Vertices:
A pyramid has vertices at the corners of the base polygon and one apex vertex at the top.
The number of vertices on the base is equal to the number of sides of the base polygon, which is $n$.
Number of vertices = (Number of vertices on the base) + (Number of apex vertices)
Number of vertices = $n + 1$
Thus, a pyramid with an n-sided base has $\mathbf{n+1}$ vertices.
Edges:
A pyramid has edges forming the sides of the base polygon and lateral edges connecting each vertex of the base to the apex.
The number of edges on the base is equal to the number of sides of the base polygon, which is $n$.
The number of lateral edges is also equal to the number of vertices on the base, which is $n$.
Number of edges = (Number of edges on the base) + (Number of lateral edges)
Number of edges = $n + n$
Number of edges = $2n$
Thus, a pyramid with an n-sided base has $\mathbf{2n}$ edges.
Summary for a pyramid with an n-sided base:
Number of Faces = $\mathbf{n+1}$
Number of Vertices = $\mathbf{n+1}$
Number of Edges = $\mathbf{2n}$
Question 87. Draw a figure that represents your mathematics textbook. What is the name of this figure? Is it a prism?
Answer:
A figure that represents your mathematics textbook would look like a three-dimensional shape with six rectangular faces, where opposite faces are identical.
The name of this figure is a Rectangular Prism or a Cuboid.
Yes, a rectangular prism is a type of prism. A prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. In the case of a rectangular prism, the base is a rectangle, and the other faces are also rectangles (which are special parallelograms), joining the corresponding sides of the two rectangular bases.
Question 88. In the given figures, identify the different shapes involved.
.png)
.png)
Answer:
In the first figure, the structure is composed of two distinct solid shapes stacked together:
The lower part, which forms the main body of the house, is a three-dimensional shape with six rectangular faces. This shape is a Rectangular Prism (also known as a Cuboid).
The upper part, forming the roof, has two parallel triangular faces and three rectangular faces connecting them. This shape is a Triangular Prism.
In the second figure, we observe a single solid shape:
This figure has two parallel triangular faces at the ends and three rectangular faces connecting the corresponding sides of these triangles. This shape is a Triangular Prism, shown resting on one of its rectangular faces.
Question 89. What figure is formed if only the height of a cube is increased or decreased?
Answer:
A cube is a special type of rectangular prism where all edges have equal length (length = width = height). If only the height of a cube is increased or decreased, the length and width remain unchanged while the height changes. This results in a three-dimensional shape with rectangular faces where the length, width, and height are not necessarily equal.
The figure formed is a Rectangular Prism or a Cuboid.
Question 90. Use isometric dot paper to draw each figure.
(a) A tetrahedron.
(b) A rectangular prism with length 4 units, width 2 units and height 2 units.
Answer:
(a) Drawing a Tetrahedron on Isometric Dot Paper:
A tetrahedron is a polyhedron with four triangular faces. To draw it on isometric paper, you can follow these steps:
1. Choose three dots on the isometric paper to form the vertices of the base triangle. Let's call them A, B, and C.
2. Connect these three points with lines to form the base triangle (e.g., triangle ABC).
3. Now, choose a fourth dot (let's call it D) that is appropriately positioned "above" the base triangle in three-dimensional space (using the third isometric direction or a combination of directions to create the sense of height and perspective).
4. Connect point D to each of the base vertices A, B, and C with lines (edges AD, BD, and CD).
5. The resulting figure with vertices A, B, C, and D and edges AB, BC, CA, AD, BD, CD represents a tetrahedron. Remember to use dashed lines for edges that would be hidden from view.
(b) Drawing a Rectangular Prism on Isometric Dot Paper (Length 4, Width 2, Height 2):
A rectangular prism has three pairs of parallel and congruent rectangular faces. To draw one with dimensions 4x2x2 on isometric paper:
1. Choose a starting point (vertex) on the isometric paper.
2. From this starting point, draw an edge of length 4 units along one of the isometric directions (e.g., horizontally to the right).
3. From the same starting point, draw an edge of length 2 units along another isometric direction (e.g., horizontally to the left/upwards). Ensure this direction is different from the first.
4. From the starting point, draw an edge of length 2 units along the third isometric direction (vertically upwards).
5. Now, from the end points of the first two edges, draw edges parallel to the third edge (the vertical one) and of length 2 units.
6. From the end points of the first and third edges, draw edges parallel to the second edge (the one of length 2 units horizontally/upwards) and of length 2 units.
7. From the end points of the second and third edges, draw edges parallel to the first edge (the one of length 4 units horizontally) and of length 4 units.
8. Connect the remaining vertices to complete the prism. You should have 8 vertices and 12 edges in total.
9. Use solid lines for visible edges and dashed lines for hidden edges to show the three-dimensional perspective correctly.
The resulting figure will be a rectangular prism with dimensions 4 units along one direction, 2 units along another, and 2 units along the third, corresponding to its length, width, and height.
Question 91. Identify the nets given below and mention the name of the corresponding solid in the space provided.
Answer:
Let's identify the solid formed by each net:
Net 1:
This net consists of a central rectangle with four other rectangles attached to its sides. When folded, the central rectangle can be the base, and the surrounding rectangles form the lateral faces. This net forms a Rectangular Prism (or Cuboid).
Net 2:
This net has a central rectangle with two triangles attached to opposite sides and two rectangles attached to the other two sides. When folded, the triangles become the parallel bases and the rectangles form the lateral faces. This net forms a Triangular Prism.
Net 3:
This net shows a square base with four triangles attached to its sides. When folded, the square forms the base and the four triangles meet at a single point above the base. This net forms a Square Pyramid.
Net 4:
This net has a rectangular base with four triangles attached to its sides. When folded, the rectangle forms the base and the four triangles meet at a single point above the base. This net forms a Rectangular Pyramid.
Net 5:
This net consists of a triangular base with three triangles attached to its sides. When folded, the base is a triangle and the three other triangles meet at a single point above the base. This net forms a Triangular Pyramid.
Net 6:
This net shows two congruent pentagons connected by five rectangles. When folded, the two pentagons form the parallel bases and the rectangles form the lateral faces connecting them. This net forms a Pentagonal Prism.
Question 92. Draw a map of your school playground. Mark all necessary places like 2 library, Playground, Medical Room, Classrooms, Assembly area, etc.
Answer:
This question requires you to draw a map.
As an AI, I cannot directly create a drawing for you. To answer this question, you need to manually draw the layout of your school playground on paper or using a drawing tool.
On your drawn map, you should clearly indicate the location and layout of the following areas:
Library
Playground
Medical Room
Classrooms (You can represent the main school building or block(s) where classrooms are located relative to the playground)
Assembly area
Ensure that the relative positions and approximate sizes of these areas are depicted on your map to provide a clear representation of your school playground and its surroundings.
Question 93. Refer to the given map to answer the following questions.

(a) What is the built-up area of Govt. Model School I ?
(b) Name the schools shown in the picture.
(c) Which park is nearest to the dispensary?
(d) To which block does the main market belong?
(e) How many parks have been represented in the map?
Answer:
(a) To determine the built-up area of Govt. Model School I, you would need to look at the portion of the map covered by the school's premises as indicated by its outline or shading. The map typically represents the area visually. Without specific units or a scale provided on the map image I can access, the built-up area is shown by the **extent of the region labelled "Govt. Model School I"** on the map.
(b) By examining the map and looking for labels containing the word "School", we can identify the schools shown. Based on the provided image, the schools shown are **Govt. Model School I** and **Govt. Model School II**.
(c) To find the park nearest to the dispensary, locate the **"Dispensary"** on the map and then visually estimate the distance to all the areas labelled as **"Park"**. The park with the shortest distance from the Dispensary on the map is the nearest one. Based on the map, the park nearest to the dispensary is **Park D**.
(d) Locate the **"Main Market"** on the map. Observe which block or area it is situated within or borders. Based on the map, the main market belongs to **Block C**.
(e) Count all the areas on the map that are labelled as **"Park"**. Based on the map, there are **Four** parks represented: Park A, Park B, Park C, and Park D.
Question 94. Look at the map given below.
Answer the following questions.
(a) Which two hospitals are opposite to each other?
(b) A person residing at Niti Bagh has to go to Chirag Delhi after dropping her daughter at Asiad Tower. Mention the important landmarks he will pass alongwith the roads taken.
(c) Name of which road is similar to the name of some month.

Answer:
(a) By observing the map, we can see that **AIIMS** and **Safdarjung Hospital** are located on opposite sides of a major road (Ring Road).
(b) To go from Niti Bagh to Chirag Delhi via Asiad Tower, the person could follow a route like this:
From **Niti Bagh**, the person can take **Aug. Kranti Marg** heading towards the Ring Road area.
They would pass by **Gulmohar Park** and cross **Siri Fort Road** before reaching the area near **Asiad Tower**. Asiad Tower is located close to **Khel Gaon Marg** and **Aug. Kranti Marg** intersects with **Ring Road** nearby.
After dropping the daughter at **Asiad Tower**, the person can continue southwards, potentially taking **Aug. Kranti Marg** further down or connecting to **Outer Ring Road** or other roads leading to **Chirag Delhi**.
Important landmarks along this route could include **Gulmohar Park**, **Siri Fort Auditorium**, **AIIMS** (visible from Ring Road), **Safdarjung Hospital** (visible from Ring Road), **Siri Fort Sports Complex**, and potentially the **IIT Delhi** area depending on the exact path near Ring Road, before heading towards Chirag Delhi.
(c) The name of the road that is similar to the name of some month is **Aug. Kranti Marg**. "Aug." is a common abbreviation for the month **August**.
Question 95. Look at the map given below.
⬜ Houses

Now answer the following questions.
(a) Name the roads that meet at round about.
(b) What is the address of the stadium?
(c) On which road is the Police Station situated?
(d) If Ritika stays adjacent to bank and you have to send her a card, what address will you write?
(e) Which sector has maximum number of houses?
(f) In which sector is Fire Station located?
(g) In the map, how many sectors have been shown?
Answer:
(a) The roads that meet at the roundabout are Park Road, Nehru Road, and Gandhi Road.
(b) The Stadium is located in Sector 3 on Stadium Road. The address of the stadium is Sector 3, Stadium Road.
(c) The Police Station is situated on Police Station Road.
(d) The Bank is located in Sector 1, on Bank Road. If Ritika stays adjacent to the bank, you would write the address as something like: Ritika, House adjacent to Bank, Bank Road, Sector 1.
(e) Counting the number of houses (represented by ⬜ symbol) in each sector:
Sector 1: 4 houses
Sector 2: 3 houses
Sector 3: 2 houses
Sector 4: 3 houses
Sector 1 has the maximum number of houses.
(f) The Fire Station is located in Sector 4.
(g) The map shows the labels for Sector 1, Sector 2, Sector 3, and Sector 4. Thus, Four sectors have been shown in the map.
Question 96. A photographer uses a computer program to enlarge a photograph. What is the scale according to which the width has enlarged?
Answer:
From the given figure, we can see the dimensions of the original photograph and the enlarged photograph.
Original width of the photograph = $3 \text{ cm}$
Width of the enlarged photograph = $9 \text{ cm}$
The scale of enlargement is given by the ratio of the new dimension to the original dimension. In this case, we consider the width:
Scale of enlargement = $\frac{\text{Width of enlarged photograph}}{\text{Original width of photograph}}$
Scale of enlargement = $\frac{9 \text{ cm}}{3 \text{ cm}}$
Scale of enlargement = $3$
The scale according to which the width has enlarged is $3$. This means the new width is 3 times the original width.
Question 97. The side of a square board is 50 cm. A student has to draw its image in her notebook. If the drawing of the square board in the notebook has perimeter of 40 cm, then by which scale the figure has been drawn?
Answer:
Given:
Side of the original square board = $50 \text{ cm}$
Perimeter of the drawing of the square board = $40 \text{ cm}$
To Find:
The scale by which the figure has been drawn.
Solution:
The perimeter of a square is given by the formula: Perimeter $= 4 \times \text{side}$.
First, let's find the perimeter of the original square board:
Perimeter of original board $= 4 \times \text{Side of original board}$
Perimeter of original board $= 4 \times 50 \text{ cm} = 200 \text{ cm}$.
Next, let's find the side length of the square drawing in the notebook using its perimeter:
Let the side of the drawing be $s_{\text{drawing}}$.
Perimeter of drawing $= 4 \times s_{\text{drawing}}$
We are given that the perimeter of the drawing is $40 \text{ cm}$.
$40 \text{ cm} = 4 \times s_{\text{drawing}}$
$s_{\text{drawing}} = \frac{40}{4} \text{ cm}$
$s_{\text{drawing}} = 10 \text{ cm}$
The scale by which the figure has been drawn is the ratio of the dimension in the drawing to the corresponding dimension in the original figure.
Scale $= \frac{\text{Side of drawing}}{\text{Side of original board}}$
Scale $= \frac{10 \text{ cm}}{50 \text{ cm}}$
Scale $= \frac{\cancel{10}^{1}}{\cancel{50}_{5}}$
Scale $= \frac{1}{5}$
The figure has been drawn using a scale of $\frac{1}{5}$. This means that $1 \text{ cm}$ in the drawing represents $5 \text{ cm}$ of the actual board.
Question 98. The distance between school and house of a girl is given by 5 cm in a picture, using the scale 1 cm : 5 km. Find the actual distance between the two places?
Answer:
Given:
Distance in the picture = $5 \text{ cm}$
Scale used = $1 \text{ cm} : 5 \text{ km}$
To Find:
The actual distance between the school and the house.
Solution:
The scale $1 \text{ cm} : 5 \text{ km}$ means that every $1 \text{ cm}$ on the picture represents an actual distance of $5 \text{ km}$.
To find the actual distance, we multiply the distance in the picture by the scale factor (which is $5 \text{ km}$ per $1 \text{ cm}$).
Actual distance = Distance in picture $\times$ Scale factor
Actual distance = $5 \text{ cm} \times \left(\frac{5 \text{ km}}{1 \text{ cm}}\right)$
Actual distance = $5 \times 5 \text{ km}$
Actual distance = $25 \text{ km}$
The actual distance between the school and the house is $25 \text{ km}$.
Question 99. Use a ruler to measure the distance in cm between the places joined by dotted lines. If the map has been drawn using the scale 1 cm :10 km, find the actual distances between
(1) School and Library
(2) College and Complex
(3) House and School
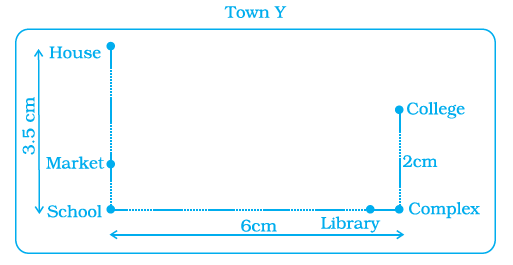
Answer:
We are given the scale of the map as $1 \text{ cm} : 10 \text{ km}$. This means that $1 \text{ cm}$ on the map represents an actual distance of $10 \text{ km}$.
To find the actual distance between the places, we need to measure the length of the dotted lines connecting them in the given image using a ruler and then use the given scale.
(1) School and Library:
Measure the length of the dotted line between School and Library on the map. Let's assume the measured distance is approximately $2 \text{ cm}$.
Distance on map $\approx 2 \text{ cm}$
Scale: $1 \text{ cm}$ on map = $10 \text{ km}$ in reality.
Actual distance = Distance on map $\times$ Scale factor
Actual distance $\approx 2 \text{ cm} \times \left(\frac{10 \text{ km}}{1 \text{ cm}}\right)$
Actual distance $\approx 2 \times 10 \text{ km}$
Actual distance $\approx 20 \text{ km}$
The actual distance between the School and the Library is approximately $20 \text{ km}$.
(2) College and Complex:
Measure the length of the dotted line between College and Complex on the map. Let's assume the measured distance is approximately $3 \text{ cm}$.
Distance on map $\approx 3 \text{ cm}$
Scale: $1 \text{ cm}$ on map = $10 \text{ km}$ in reality.
Actual distance = Distance on map $\times$ Scale factor
Actual distance $\approx 3 \text{ cm} \times \left(\frac{10 \text{ km}}{1 \text{ cm}}\right)$
Actual distance $\approx 3 \times 10 \text{ km}$
Actual distance $\approx 30 \text{ km}$
The actual distance between the College and the Complex is approximately $30 \text{ km}$.
(3) House and School:
Measure the length of the dotted line between House and School on the map. Let's assume the measured distance is approximately $4 \text{ cm}$.
Distance on map $\approx 4 \text{ cm}$
Scale: $1 \text{ cm}$ on map = $10 \text{ km}$ in reality.
Actual distance = Distance on map $\times$ Scale factor
Actual distance $\approx 4 \text{ cm} \times \left(\frac{10 \text{ km}}{1 \text{ cm}}\right)$
Actual distance $\approx 4 \times 10 \text{ km}$
Actual distance $\approx 40 \text{ km}$
The actual distance between the House and the School is approximately $40 \text{ km}$.
Question 100. The actual length of a painting was 2 m. What is its length in the photograph if the scale used is 1 mm : 20 cm.

Answer:
Given:
Actual length of the painting = $2 \text{ m}$
Scale used = $1 \text{ mm} : 20 \text{ cm}$
To Find:
The length of the painting in the photograph.
Solution:
First, we need to make the units consistent. The scale is given in millimeters and centimeters. Let's convert the actual length of the painting from meters to centimeters.
$1 \text{ m} = 100 \text{ cm}$
Actual length of the painting = $2 \text{ m} = 2 \times 100 \text{ cm} = 200 \text{ cm}$.
The scale $1 \text{ mm} : 20 \text{ cm}$ means that an actual length of $20 \text{ cm}$ is represented by $1 \text{ mm}$ in the photograph.
We can set up a proportion to find the length in the photograph. Let the length in the photograph be $x \text{ mm}$.
$\frac{\text{Length in photograph}}{\text{Actual length}} = \frac{\text{Scale length in photo}}{\text{Scale length in reality}}$
$\frac{x \text{ mm}}{200 \text{ cm}} = \frac{1 \text{ mm}}{20 \text{ cm}}$
To find $x$, we can multiply both sides by $200 \text{ cm}$:
$x \text{ mm} = \frac{1 \text{ mm}}{20 \text{ cm}} \times 200 \text{ cm}$
The unit 'cm' cancels out:
$x \text{ mm} = \frac{1}{20} \times 200 \text{ mm}$
$x \text{ mm} = \frac{200}{20} \text{ mm}$
$x \text{ mm} = 10 \text{ mm}$
The length of the painting in the photograph is $10 \text{ mm}$.
Question 101. Find the scale.
(a) Actual size 12 m
Drawing size 3 cm
(b) Actual size 45 feet
Drawing size 5 inches
Answer:
(a) Finding the scale for Actual size 12 m and Drawing size 3 cm:
The scale is the ratio of the drawing size to the actual size.
To find the scale, we need to express both sizes in the same units. Let's convert meters to centimeters, since $1 \text{ m} = 100 \text{ cm}$.
Actual size = $12 \text{ m} = 12 \times 100 \text{ cm} = 1200 \text{ cm}$.
Drawing size = $3 \text{ cm}$.
Scale $= \frac{\text{Drawing size}}{\text{Actual size}}$
Scale $= \frac{3 \text{ cm}}{1200 \text{ cm}}$
Simplify the fraction:
Scale $= \frac{\cancel{3}^{1}}{\cancel{1200}_{400}}$
Scale $= \frac{1}{400}$
The scale can be expressed as the ratio $1:400$.
Alternatively, we can express the scale in terms of units: $3 \text{ cm}$ represents $12 \text{ m}$. Dividing both sides by 3 to find what $1 \text{ cm}$ represents:
$1 \text{ cm} : \frac{12}{3} \text{ m}$
$1 \text{ cm} : 4 \text{ m}$
So, the scale is $\mathbf{1:400}$ or $\mathbf{1 \text{ cm} : 4 \text{ m}}$.
(b) Finding the scale for Actual size 45 feet and Drawing size 5 inches:
To find the scale, we need to express both sizes in the same units. Let's convert feet to inches, since $1 \text{ foot} = 12 \text{ inches}$.
Actual size = $45 \text{ feet} = 45 \times 12 \text{ inches} = 540 \text{ inches}$.
Drawing size = $5 \text{ inches}$.
Scale $= \frac{\text{Drawing size}}{\text{Actual size}}$
Scale $= \frac{5 \text{ inches}}{540 \text{ inches}}$
Simplify the fraction:
Scale $= \frac{\cancel{5}^{1}}{\cancel{540}_{108}}$
Scale $= \frac{1}{108}$
The scale can be expressed as the ratio $1:108$.
Alternatively, we can express the scale in terms of units: $5 \text{ inches}$ represents $45 \text{ feet}$. Dividing both sides by 5 to find what $1 \text{ inch}$ represents:
$1 \text{ inch} : \frac{45}{5} \text{ feet}$
$1 \text{ inch} : 9 \text{ feet}$
So, the scale is $\mathbf{1:108}$ or $\mathbf{1 \text{ inch} : 9 \text{ feet}}$.
Question 102. In a town, an ice cream parlour has displayed an ice cream sculpture of height 360 cm. The parlour claims that these ice creams and the sculpture are in the scale 1:30. What is the height of the ice creams served?
Answer:
Given:
Capacity (Volume) of the cylindrical tank, $V = 1.54 \text{ m}^3$
Height of the cylindrical tank, $h = 90 \text{ cm}$
To Find:
The radius of the base of the tank, $r$.
Solution:
The formula for the volume of a cylinder is $V = \pi r^2 h$, where $V$ is the volume, $r$ is the radius of the base, and $h$ is the height.
First, we need to ensure all units are consistent. The volume is in cubic meters ($\text{m}^3$), and the height is in centimeters ($\text{cm}$). Let's convert the height from centimeters to meters.
$1 \text{ m} = 100 \text{ cm}$
$h = 90 \text{ cm} = \frac{90}{100} \text{ m} = 0.9 \text{ m}$
Now, substitute the given values into the volume formula. We will use the approximation $\pi \approx \frac{22}{7}$.
$V = \pi r^2 h$
$1.54 \text{ m}^3 = \frac{22}{7} \times r^2 \times 0.9 \text{ m}$
Now, we need to solve for $r^2$:
$r^2 = \frac{1.54 \times 7}{22 \times 0.9}$
$r^2 = \frac{10.78}{19.8}$
To simplify the fraction, we can multiply the numerator and denominator by 100 to remove decimals:
$r^2 = \frac{1078}{1980}$
Now, simplify the fraction by dividing by common factors. Both are divisible by 2:
$r^2 = \frac{539}{990}$
Both 539 and 990 are divisible by 11 ($539 = 11 \times 49$, $990 = 11 \times 90$).
$r^2 = \frac{49}{90}$
Now, take the square root of both sides to find $r$:
$r = \sqrt{\frac{49}{90}} \text{ m}$
$r = \frac{\sqrt{49}}{\sqrt{90}} \text{ m}$
$r = \frac{7}{\sqrt{90}} \text{ m}$
We can simplify $\sqrt{90}$: $\sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} = 3\sqrt{10}$.
$r = \frac{7}{3\sqrt{10}} \text{ m}$
To rationalize the denominator, multiply the numerator and denominator by $\sqrt{10}$:
$r = \frac{7\sqrt{10}}{3\sqrt{10}\sqrt{10}} \text{ m}$
$r = \frac{7\sqrt{10}}{3 \times 10} \text{ m}$
$r = \frac{7\sqrt{10}}{30} \text{ m}$
Alternatively, we can express the radius in centimeters by converting the result:
$r = \frac{7\sqrt{10}}{30} \text{ m} \times \frac{100 \text{ cm}}{1 \text{ m}}$
$r = \frac{7\sqrt{10} \times \cancel{100}^{10}}{\cancel{30}^{3}} \text{ cm}$
$r = \frac{70\sqrt{10}}{3} \text{ cm}$
Based on the given values, the radius of the base of the tank is $\frac{7\sqrt{10}}{30} \text{ m}$ or $\frac{70\sqrt{10}}{3} \text{ cm}$.
Note: It is possible that the question intended the volume or height values to be slightly different such that the radius resulted in a simpler number, like $0.7 \text{ m}$ (which would yield a volume of $1.386 \text{ m}^3$ for $h=0.9 \text{ m}$ using $\pi = 22/7$) or $1 \text{ m}$ height (which would yield $V = 1.54 \text{ m}^3$ for $r=0.7 \text{ m}$). However, calculating directly from the provided numbers gives $r^2 = 49/90$.

